Entropy

Entropy & Clausius Inequality

Entropy is a property

• A measure of the degree of microscopic disorder in the system
• Entropy can be transferred by heat but not by work
• Entropy is not conserved
• Entropy can be generated/created but not destroyed
• Total entropy for isolated systems (system + surroundings) increases for all real processes

Clausius Inequality

Cyclic integral of 𝛿𝑄/𝑇 is always less than or equal to zero for all cycles regardless of reversible, irreversible cycles $\oint \frac{\delta Q}{T}\le 0$

• Unit for T must be absolute temperature

For reversible cycles

Example: Carnot Heat Engine $\oint {\frac{\delta Q}{T}}_{rev}=0$

For irreversible cycles

Example: Any other heat engine $\oint {\frac{\delta Q}{T}}_{irrev}<0$

Generally, cyclic integrals of any property is zero

Hence Entropy is a property: $dS={\left(\frac{\delta Q}{T}\right)}_{\text{int rev}}(\text{kJ/K})$

---

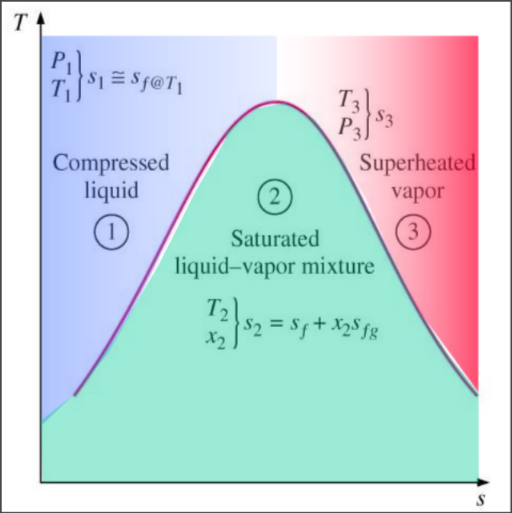
Entropy of Pure Substances

Entropy data for pure substances (including real gases) can be obtained from property tables

Obtaining Entropy change (using property table)

The difference between the entropy of the initial state vs the finals state $\Delta S=S_2-S_1=m(s_2-s_1)$ ** Interpolation may be needed

---

Property Diagrams Involving Entropy

2nd Law analysis: T-s & h-s diagrams

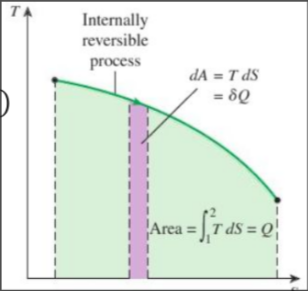
Analysing T-s Diagrams

Differential form of entropy:

$$dS={\left(\frac{\delta Q}{T}\right)}_{\text{int rev}}(\text{kJ/K})\to \delta Q_{\text{int rev}}=TdS(\text{kJ})$$

$\text{Or: }\delta q_{\text{int rev}}=Tds(\text{kJ/kg})$ Integrating entropy: $Q_{\text{int rev}}={\int }_1^{2}TdS(\text{kJ})q_{\text{int rev}}={\int }_1^{2}Tds(\text{kJ/kg})$

Tip

Area under the process curve in the T-s diagram represents the heat transfer in an internally reversible process!

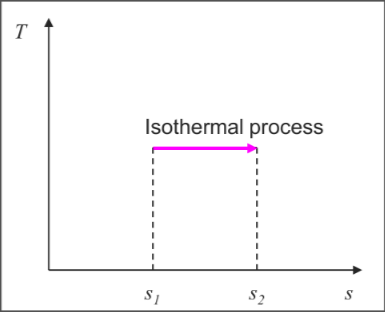
Special conditions

Internally reversible isothermal process

$Q_{\text{int rev}}=T_0\Delta S(\text{kJ})$ $q_{\text{int rev}}=T_0\Delta s(\text{kJ/kg})$

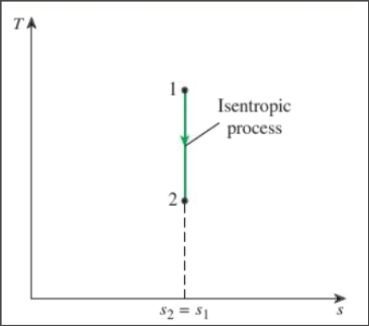
Isentropic process

Constant entropy — vertical line segment

---

Tds Relations (Entropy change without Property table)

1st Tds Equation (Gibbs Equation)

$TdS=dU+PdV\text{or}\boxed{Tds=du+Pdv}$

Expand for Derivation

2nd Tds Equation

$Tds=dh-vdP$ Alternative forms: $\boxed{ds=\frac{du}{T}+\frac{Pdv}{T}}\boxed{ds=\frac{dh}{T}-\frac{vdP}{T}}$

Expand for Derivation

---

Entropy Change of Liquids & Solids

Liquids and solids can be approximated as incompressible substances, hence:

• 𝑑𝑣 ≅ 0
• $ds=\frac{du}{T}+\frac{\cancel{Pdv}}{\cancel{T}}⟶ds=\frac{du}{T}=\frac{cdT}{T}$
• $c_p=c_v=c⟶du=cdT$

Thus, the formula:

$s_2-s_1={\int }_1^{2}c(T)\frac{dT}{T}\approx c_{\text{avg}}\ln \frac{T_2}{T_1}\text{(kJ/kg}\cdot \text{K)}$

• Entropy change for liquids and solids are only dependent on temperature and independent of pressure

For isentropic

$\Delta s=0,\Delta T=0$

---

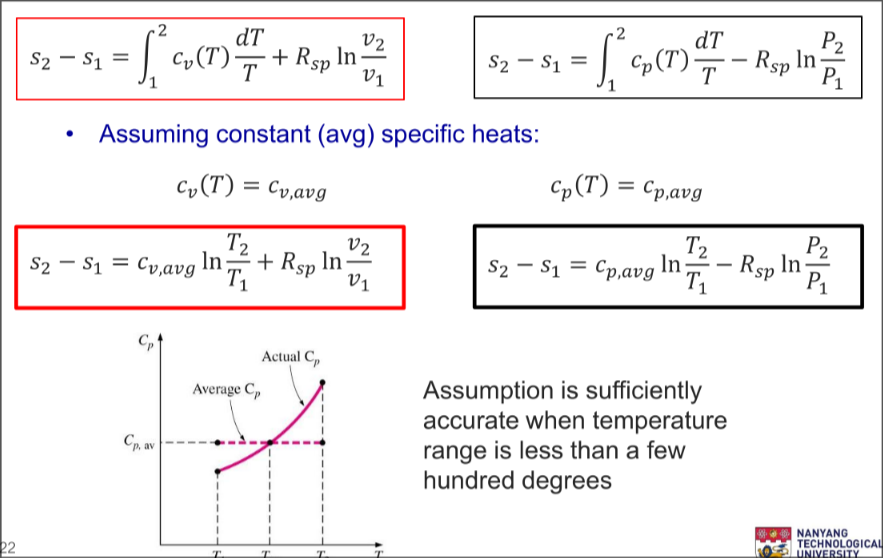
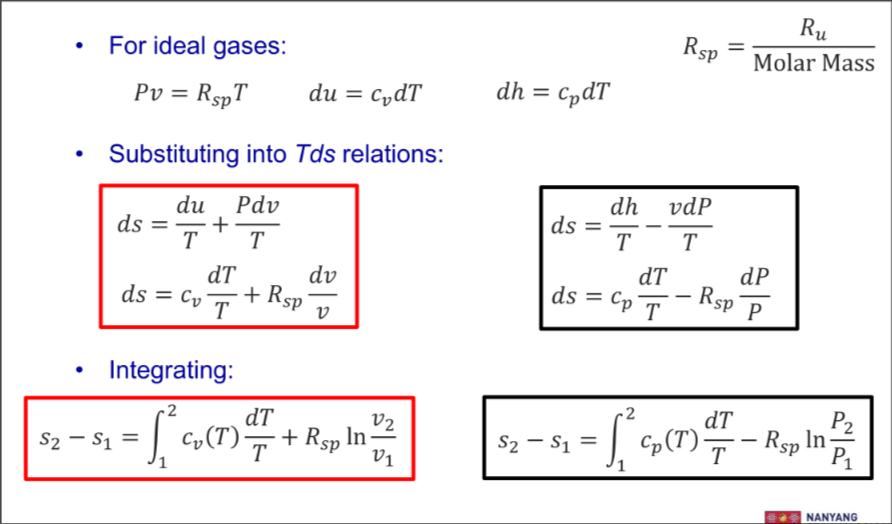
Entropy Change of Ideal Gases

Ideal gas equations

$Pv=R_{sp}TPV=m{R}_{sp}TPV=n{R}_{u}Tdu=c_{v}dTdh=c_{p}dT$

where:

$R_u=8.314J/mol\cdot K{R}_{sp}=\frac{R_u}{\text{Molar Mass}}$

Thus, the formulas:

$\boxed{s_2-s_1=c_{v,avg}\ln \frac{T_2}{T_1}+R_{sp}\ln \frac{v_2}{v_1}}\boxed{s_2-s_1=c_{p,avg}\ln \frac{T_2}{T_1}-R_{sp}\ln \frac{P_2}{P_1}}$ Note: $c_{avg}\ne ½(c_1+c_2)$ $c_{avg}=c@T_{avg}$

Expand for Derivation

For isentropic

$\Delta s=0$

From 1st Tds equation

$\boxed{{\left(\frac{T_2}{T_1}\right)}_{isen}={\left(\frac{v_1}{v_2}\right)}^{k-1}}$

Expand for Derivation

From 2nd Tds equation

$\boxed{{\left(\frac{T_2}{T_1}\right)}_{isen}={\left(\frac{P_2}{P_1}\right)}^{\frac{k-1}{k}}}$

Expand for Derivation

Combined

$\boxed{{\left(\frac{P_2}{P_1}\right)}_{isen}={\left(\frac{v_1}{v_2}\right)}^k}\text{or}\boxed{P{v}^k=\text{const}}$

---

Entropy Change for Reversible Processes

Internally reversible isothermal heat transfer

$\Delta S={\int }_1^2{\left(\frac{\delta Q}{T}\right)}_{\text{int rev}}={\int }_1^2{\left(\frac{\delta Q}{T_0}\right)}_{\text{int rev}}=\frac{1}{T_0}{\int }_1^2(\delta Q{)}_{\text{int rev}}$ $\boxed{\Delta S=\frac{Q}{T_0}\text{(kJ/K)}}$

• Where T0 is the constant temperature (K), Q is the heat transfer for the internally reversible process
• Commonly used to determine the entropy change of thermal energy reservoirs that supply/absorb heat indefinitely at constant temperature

---

Entropy Change for Irreversible Processes

For irreversible process, the entropy change can be determined along an imaginary internally reversible path

Entropy Change

Additional entropy change due to presence of irreversibilities

• Always positive (irreversible) or zero (reversible)
• Not a property; value is process dependent

$\Delta S_{sys}={\int }_1^2\frac{\delta Q}{T}+S_{gen}$

\text{Entropy change of} &= \text{Entropy transfer} + \text{Entropy generation} \\ \text{a closed system} &\quad \text{due to heat transfer} \quad \text{due to irreversibilities} \end{align}$$ ## Differential form $$ dS \geq \frac{\delta Q}{T}$$ > [!NOTE]- Expand for Derivation > > ![[Pasted image 20250916132408.png]] --- # Entropy Change for Systems $$\begin{aligned} &\boxed{\Delta S_{system} = S_{in} - S_{out} + S_{gen}} \\[1em] \text{Change in total} &= \text{Total} - \text{Total} + \text{Total} \\ \text{entropy of the} &\quad \text{entropy} \quad \text{entropy} \quad \text{entropy} \\ \text{system} &\quad \text{entering} \quad \text{leaving} \quad \text{generated} \end{aligned}$$ ### Entropy Changes Entropy change is zero in steady flow devices during steady operation (turbines, compressors, pumps, nozzles, diffusers, heat exchangers etc.) $$\Delta S_{system} = S_{final} - S_{initial} = 0$$ ### Entropy Transfer For closed systems, entropy is transferred only by heat $$S_{in} - S_{out} = \int_1^2 \frac{\delta Q}{T} \cong \sum \frac{Q_k}{T_k}$$ $$Q_{in} \xrightarrow{\text{}} \boxed{\begin{array}{c} \text{Closed} \\ \text{System} \end{array}} \xrightarrow{\text{}} Q_{out}$$ - $Q_k$ = heat transfer - $T_k$ = boundary temperature through which heat is transferred ### Entropy Generation A measure of entropy created by irreversibilities during a process (friction, heat transfer via finite temperature difference, mixing etc.) $$S_{gen} \begin{cases} > 0 & \text{irreversible process} \\ = 0 & \text{reversible process} \\ < 0 & \text{impossible process} \end{cases}$$ ## Entropy Change — Closed Systems $$\Delta S_{closed} = S_2 - S_1 = \sum \frac{Q_k}{T_k} + S_{gen}$$ - $Q_k$ = heat transfer - $T_k$ = boundary temperature through which heat is transferred ### Special case — adiabatic system Change in entropy is only due to entropy generation within the system boundaries $$\Delta S_{closed} = S_2 - S_1 = \cancel{\sum \frac{Q_k}{T_k}} + S_{gen}$$ $$\Delta S_{adiabatic\ system} = S_{gen} > 0$$ - Since entropy generation for irreversible processes can never be less than zero, the entropy in an adiabatic closed system always increases ### Special case — isentropic process $$ \Delta s =0 \quad \rightarrow \quad \Delta S_{isen} = S_2 - S_1 = \cancel{\sum \frac{Q_k}{T_k}} + \cancel{S_{gen}} $$ - *Isentropic = Reversible Adiabatic Process* ### Special case - Isolated systems No mass, heat or work transfer for an isolated system $$\Delta S_{isolated} = S_2 - S_1 = \cancel{\sum \frac{Q_k}{T_k}} + S_{gen}$$ $$\Delta S_{isolated} = S_{gen} > 0$$ An isolated systems may consist of any number of subsystems; total entropy = sum of its parts $$\Delta S_{total} = \sum_{i=1}^{N} \Delta S_i > 0$$ --- # Entropy Change for Flow Control Volumes $$(S_2 - S_1)_{CV} = \sum m_i s_i - \sum m_e s_e + \sum \frac{Q_k}{T_k} + S_{gen}$$ $$ \text{Change in Entropy} = \text{Net entropy transfer by heat and mass flow}+\text{Entropy generation}$$ Rate Form: $$\dot{S}_{CV} = \sum \dot{m}_i s_i - \sum \dot{m}_e s_e + \sum \frac{\dot{Q}_k}{T_k} + \dot{S}_{gen}$$ ![[Pasted image 20250916213327.png|400]] ## Steady State, Steady Flow situation $$\boxed{\sum_k \frac{\dot{Q}_k}{T_k} + \dot{S}_{gen} + \sum_i \dot{m}_i s_i - \sum_e \dot{m}_e s_e = 0}$$ - rate of entropy change is 0 > [!NOTE] Recap: Energy balance for heat exchanger (flow control volume) > > $$\sum \dot{m}_i h_i - \sum \dot{m}_e h_e + \dot{Q} - \dot{W} = 0$$ ## Single Stream, Steady Flow $$\dot{m}_i = \dot{m}_e = \dot{m}$$ $$\dot{m}(s_e - s_i) = \sum \frac{\dot{Q}_k}{T_k} + \dot{S}_{gen}$$ ### Adiabatic - Entropy of fluid will increase as it flows through an adiabatic device $$\dot{m}(s_e - s_i) = \cancel{\sum {\frac{\dot{Q}_k}{T_k}}} + \dot{S}_{gen}$$ $$\dot{S}_{gen} \geq 0 \quad \rightarrow s_e \geq s_i$$ ### Adiabatic & Reversible → Isentropic Flow $$\dot{m}(s_e - s_i) = \cancel{\sum \frac{\dot{Q}_k}{T_k}} + \cancel{\dot{S}_{gen}}$$ $$\rightarrow s_e = s_i$$ --- # Reversible Steady Flow Work When $\Delta ke \approx 0$ & $\Delta pe \approx 0$: $$w_{rev} = -\int_i^e v \, dP$$ - W is positive → work done by fluid > [!NOTE]- Expand for Derivation > > ![[Pasted image 20250916231137.png]] ## Special case — Incompressible fluid When v is constant & $\Delta ke \approx 0$ & $\Delta pe \approx 0$: $$w_{rev} = -v(P_2 - P_1)$$ ## Special case — Fluid does no work and incompressible (eg. pipes) $$0 = -v(P_2 - P_1) - \frac{V_2^2 - V_1^2}{2} - g(z_2 - z_1) \quad \text{Bernoulli Equation}$$ - V represents fluid velocity as opposed to specific volume --- # Polytropic Work in Steady Flow Devices $$w_{poly} = -\int_1^2 v \, dP = -\int_1^2 \left(\frac{C}{P}\right)^{1/n} dP$$ $$= -\frac{n}{n-1}(P_2 v_2 - P_1 v_1)$$ Polytropic means:

Pv^n = \text{const.}$$

For Ideal Gas

$w_{poly}=-\frac{n{R}_{sp}(T_2-T_1)}{n-1}=-\frac{n{R}_{sp}{T}_1}{n-1}\left[{\left(\frac{P_2}{P_1}\right)}^{(n-1)/n}-1\right]$

Isentropic for Ideal Gas (n=k)

Due to the rule that $p{v}^k=\text{const}$ for isentropic $w_{s=\text{const}}=-\frac{k{R}_{sp}(T_2-T_1)}{k-1}=-\frac{k{R}_{sp}{T}_1}{k-1}\left[{\left(\frac{P_2}{P_1}\right)}^{(k-1)/k}-1\right]$

Isothermal (n=1)

$w_{T=\text{const}}=-R_{sp}T\ln \frac{P_2}{P_1}$

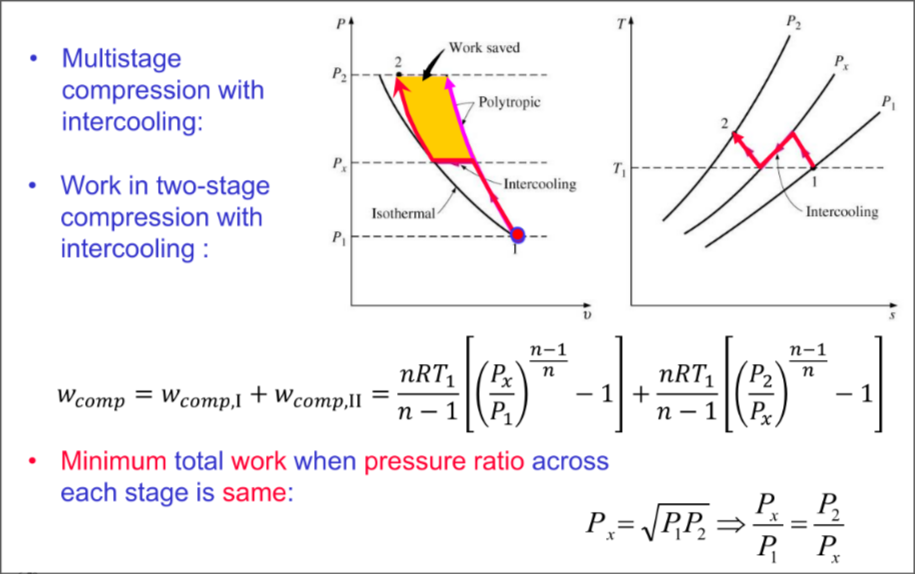
Min Compressor Work

---

Steady State Control Volume Devices

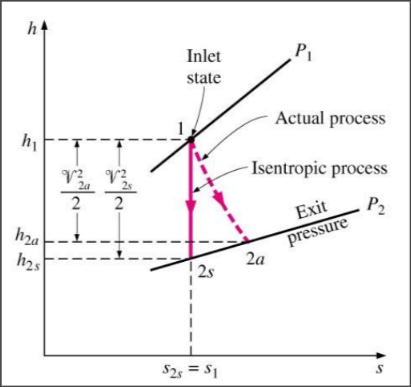
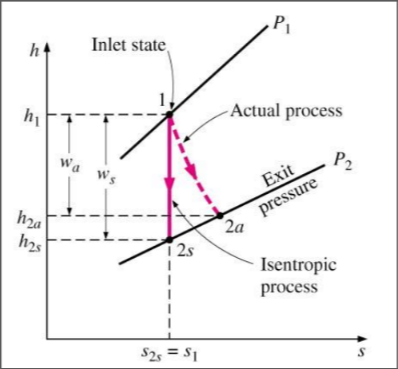
SSCV devices are near adiabatic and work best when irreversibilities are minimized, making isentropic processes the ideal models for these devices.

Isentropic efficiency

The measure of the deviation of the actual (adiabatic) process from the idealized one

---

Isentropic Efficiency for Turbines

${\eta }_T=\frac{\text{Actual work}}{\text{Isentropic work}}=\frac{w_a}{w_s}{\eta }_T\cong \frac{h_1-h_{2a}}{h_1-h_{2s}}$ $\text{Where,}{w}_T=h_1-h_2$

• ${\eta }_T\approx$ 90% for large turbines
• ${\eta }_T\approx$ 70% for small turbines

---

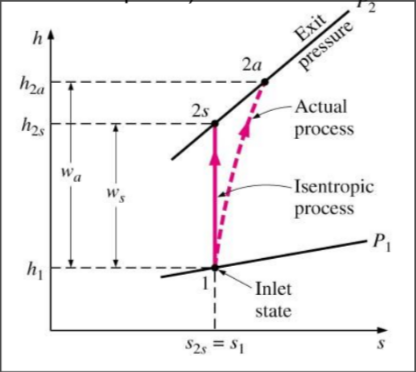
Isentropic Efficiency for Compressors

${\eta }_C=\frac{\text{Isentropic work}}{\text{Actual work}}=\frac{w_s}{w_a}{\eta }_C\cong \frac{h_{2s}-h_1}{h_{2a}-h_1}$ where, $w_c=-(h_1-h_2)$

• power consumed in isentropic is lower than actual
• ${\eta }_C\approx$ 75-85% for well designed

Isentropic efficiency for Pumps

${\eta }_P=\frac{w_s}{w_a}\cong \frac{v(P_2-P_1)}{h_{2a}-h_1}$

---

Isentropic Efficiency for Nozzles

${\eta }_N=\frac{\text{Actual KE @ exit}}{\text{Isen. KE @ exit}}=\frac{V_{2a}^2}{V_{2s}^2}$ $h_1-h_{2a}=\frac{V_{2a}^2}{2}$ ${\eta }_N=\frac{h_1-h_{2a}}{h_1-h_{2s}}=\frac{c_{p,avg}(T_1-T_{2a})}{c_{p,avg}(T_1-T_{2s})}$

• V represents fluid velocity
• Typical ${\eta }_N\approx 90-95percent$

---

References