Engineering Materials

Structure of Crystalline Solids

Crystalline structures

• Seven crystal systems

  

  

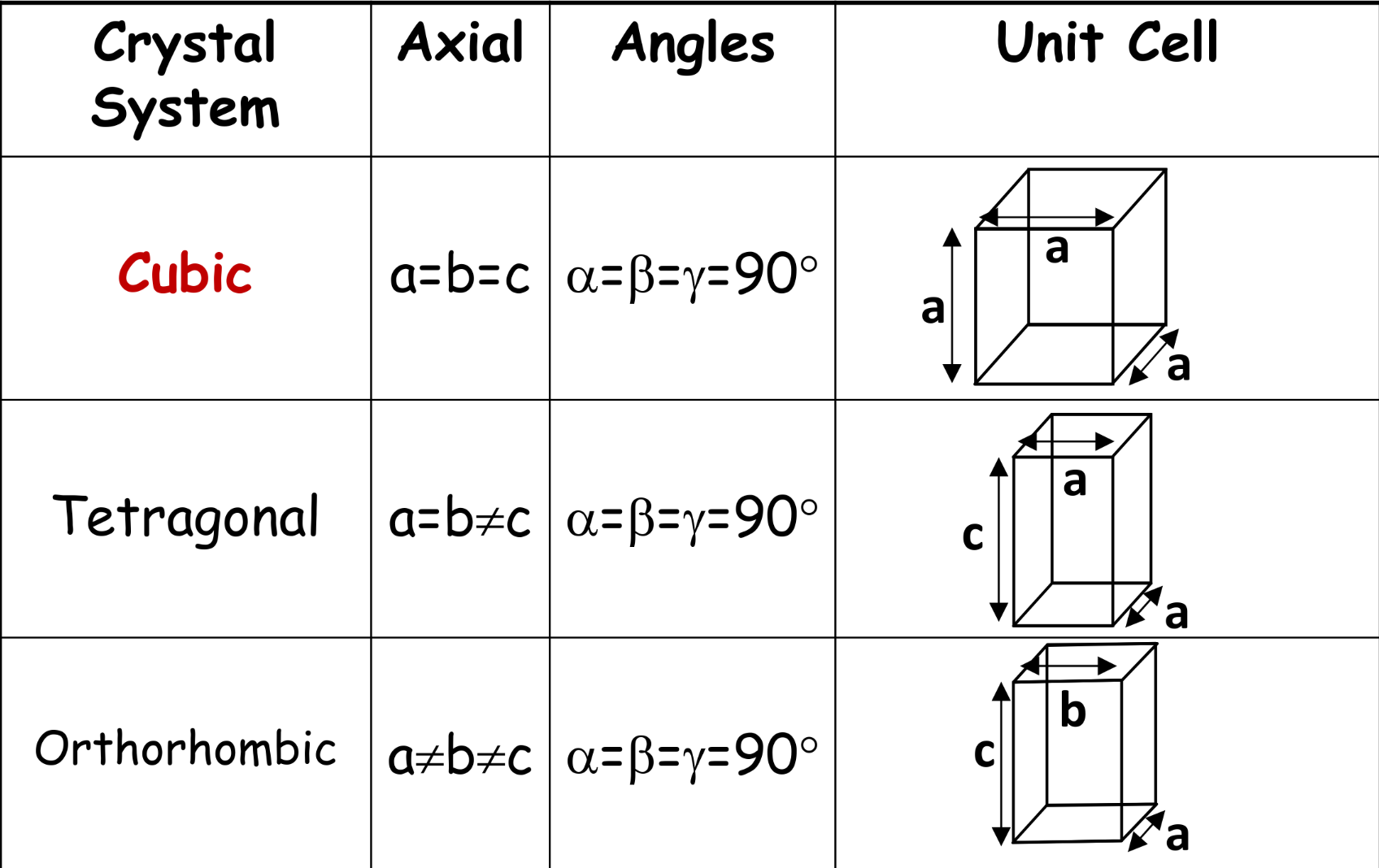
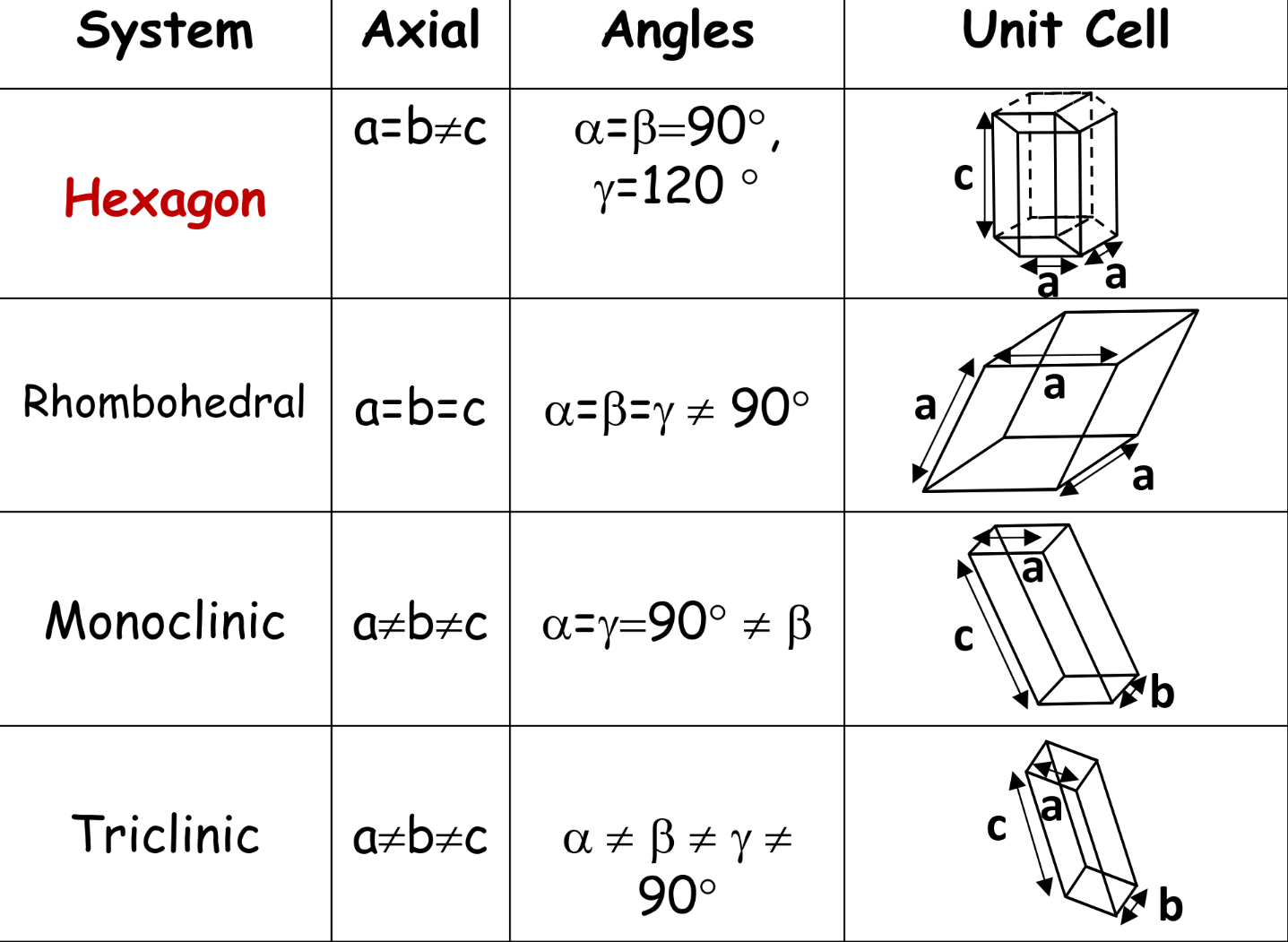
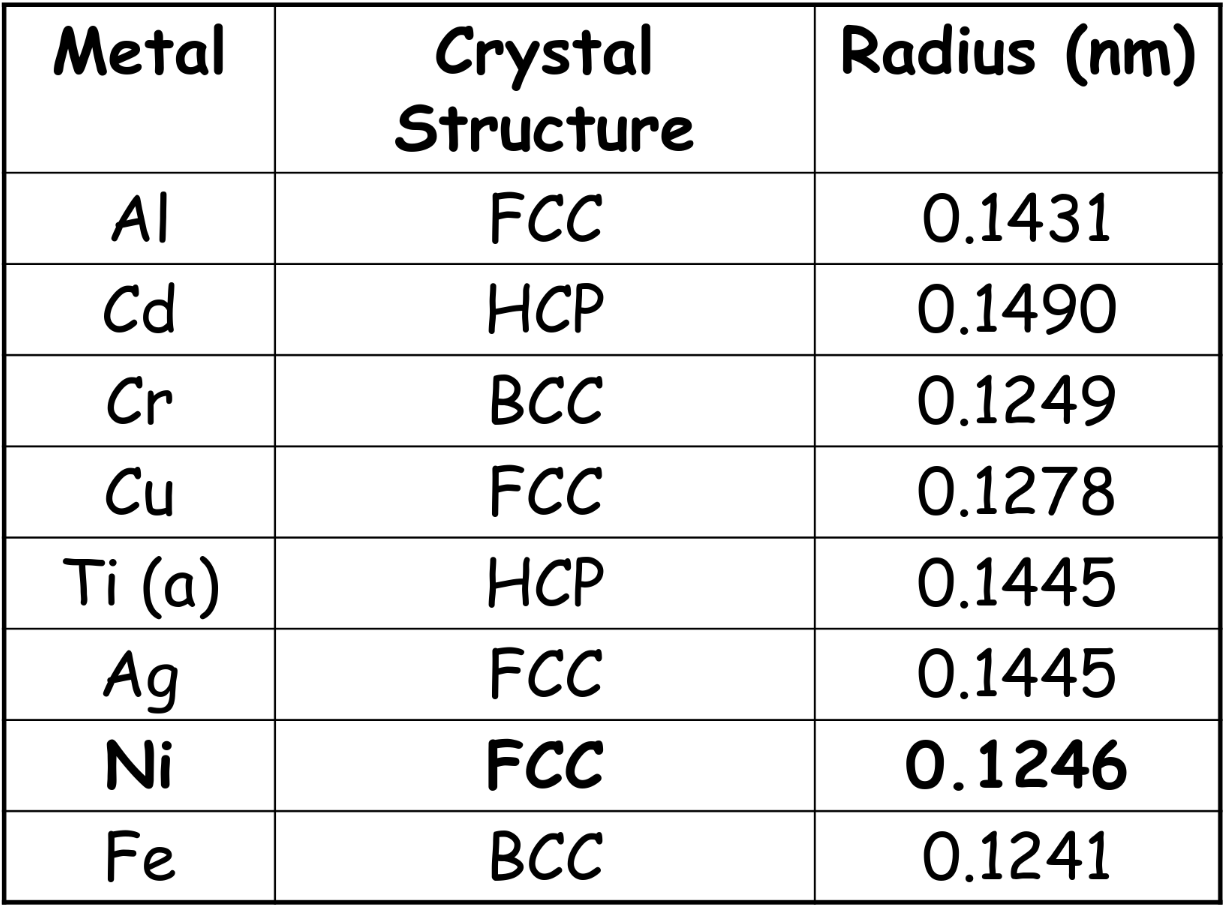
• Common metal’s structure — Generally FCC, BCC and HCP

  

Simple Cubic

Cubic unit cell — atoms only at corners

• 1 atom per unit cell

  

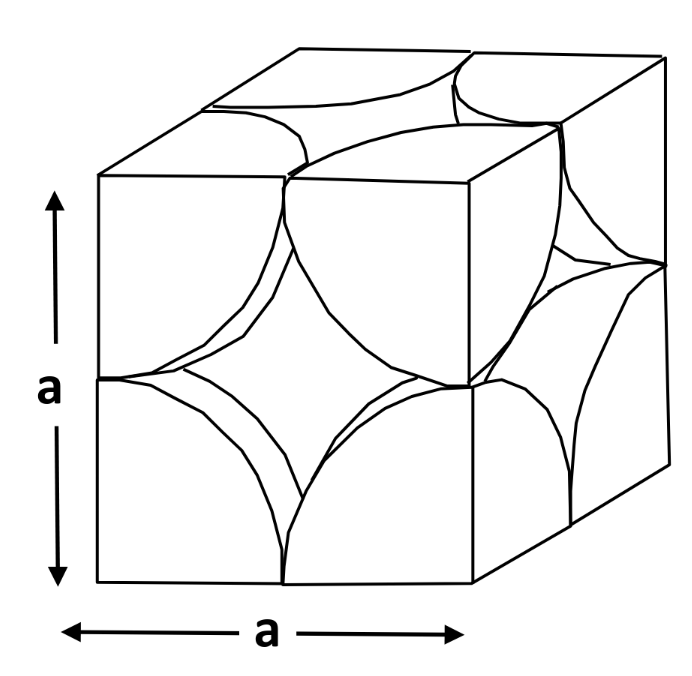
Body-Centered Cubic (BCC)

Cubic unit cell — atoms at corners and single atom at center

• Unit cell edge length (a) & atomic radius (R) is related

  

$a=\frac{4R}{\sqrt{3}}$

• 2 atom per unit cell — Coordination no. = 8 — APF = 0.68

APF (Atomic packing fraction) = density of atoms

CN (Coordination number) = number of neighbouring atoms touching an atom at a time

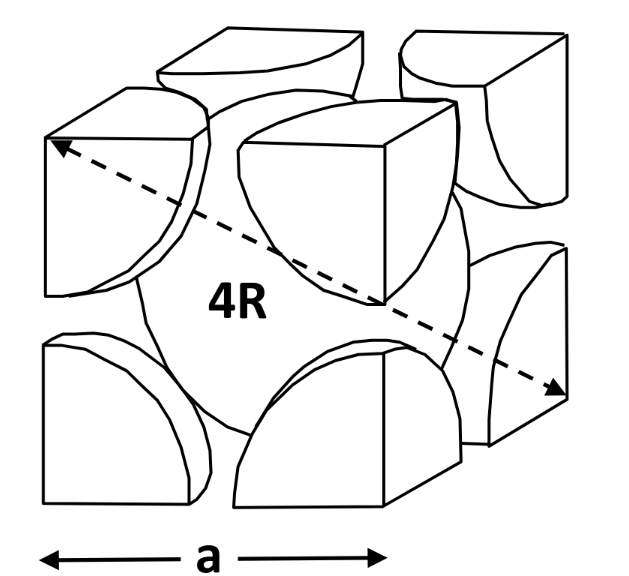
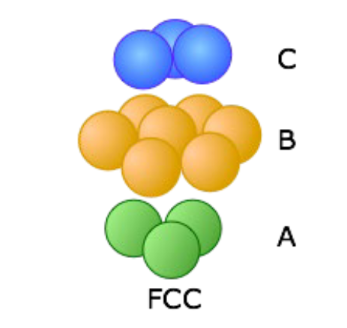
Face-Centered Cubic (FCC)

Cubic unit cell — atoms at corners and center of cube faces

• Structure

  

$a=2R\sqrt{2}$

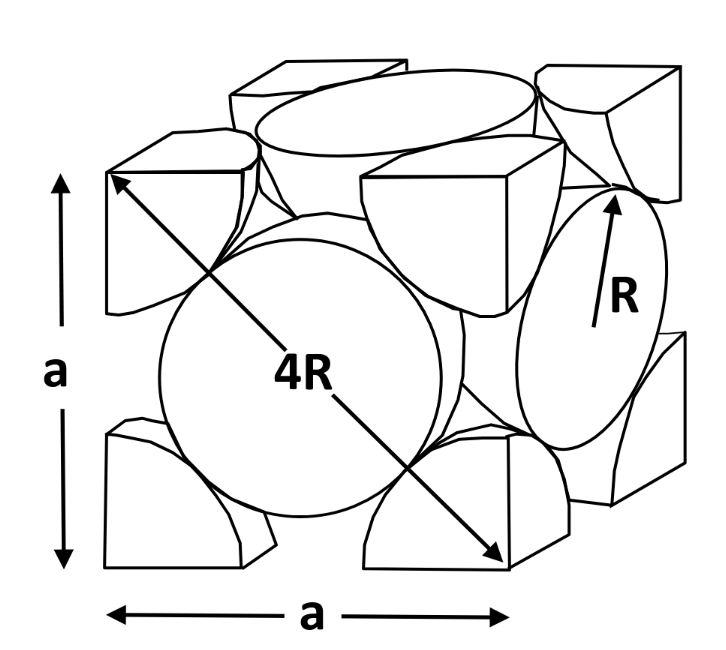
• 4 atom per cell — coordination no. = 12 — APF = 0.74

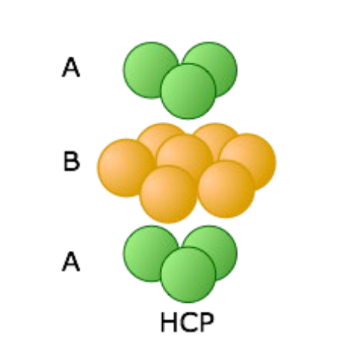
Hexagonal Closed Packing (HCP)

Hexagonal unit cell

• Structure (c/a < 1.633)

  

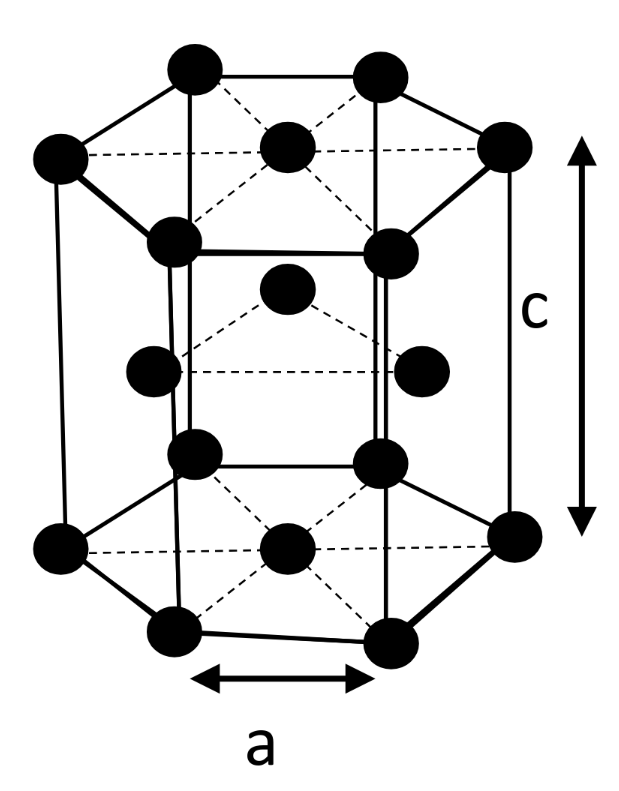
• Coordination number 12 — APF = 0.74

Stacking & Packing Structures

• ABA stacking

  

• ABC stacking

  

Density of Unit Cell (p)

$p=\frac{n\ast A_m}{N_A\ast V_C}$ n = atom per unit cell $N_a$ = Avogadro’s number (6.023 x 10^23)

$A_m$ = Atomic mass $V_C$ = Volume of unit cell

Crystallographic Parameters

Crystallographic Direction

Important

• Bar above number indicates negative value $[\bar{u},v,w]$
• Scale value to ≤ 1 for sketching Families of directions : vectors with the same magnitude
• symbolised by
• parallel directions are not unique

Crystallographic Planes

Set of parallel and equally spaced planes that pass through the centers of atoms in crystals where no centers are situated between planes

Miller indices: Symbolic vector representation for the orientation of an atomic direction or plane in a crystal lattice

• Described as (h k l) where “h,k & l” are miller indices
• Metal deformation are dependent on sliding of these planes — transportation of heat and electrons are also affected by them Miller indices for given plane
• Plane cannot touch origin / new origin — based on closest corner
• Find intercepts — reciprocal for plane miller indices
• E.g. intercept = -1 , -1/2, 1 → $(\bar{1}\bar{2}1)$ Draw plane given miller indices
• Reciprocal to find intercepts Family of planes

Crystallographically equivalent — Same packing density, atomic environment, physical & mechanical properties

• Indicated by {h k l}
• For cubic systems only, same indices = family
  • (100) (010) ($\bar{1}$,0,0) — same family {100}

Linear Density

$LD=\frac{No.ofatomscenteredondirectionalvector}{Lengthofdirectionalvector}$

End point of vector does not cut the center

Planar Density

$PD=\frac{\text{No. of atoms centered on a plane}}{\text{Area of plane}}$

• Only area of atom within the plane is considered

Properties of Crystalline Solids

Defects in Solids

Point defects

Vacancies: site where atom is missing in lattice Self-interstitial: ‘extra’ atom between lattice site

The crystal structure aims to minimise strain, and thus the energy of the system (Gibbs free energy G), dependent on:

• Enthalpy (H): energy cost to break atomic bonds forming defect
• Entropy (TS): energy associated with no. of possible states $G=H-TS$ Equilibrium concentration of vacancies @ T = constant (≠0) ARRHENIUS LAW $\frac{n}{N}=e^{(-\frac{Q_v}{kT})}$ n = number of defects — N = Number of atomic sites $Q_v$ = activation energy of vacancy formation [J/mol.] or [eV/atom] k = Boltzmann’s constant, 1.38 x 10^-23 [J/atom/K] or 8.62 x 10^-5 [eV/atom/K]

---

Impurity(Alloy) — Interstitial & Substitutional Interstitial site positions in FCC:

• Octahedral — 1/2 1/2 1/2 — 0 1/2 1
• Tetrahedral — 1/4 3/4 1/4 Interstitial site positions in BCC:
• Octahedral — 1/2 1 0
• Tetrahedral — 1 1/2 1/4

---

Creation of point defects

• Annealing and abrupt quenching: “kinetically trapped point defects”
• Irradiation by high energy particles
• Ion implantation: useful for controlled doping of semiconductors
• Cold working

Line defects - dislocations

Burgers vector (b) — defines the magnitude and direction of lattice distortion of a dislocation

• Edge dislocations $\perp$

  

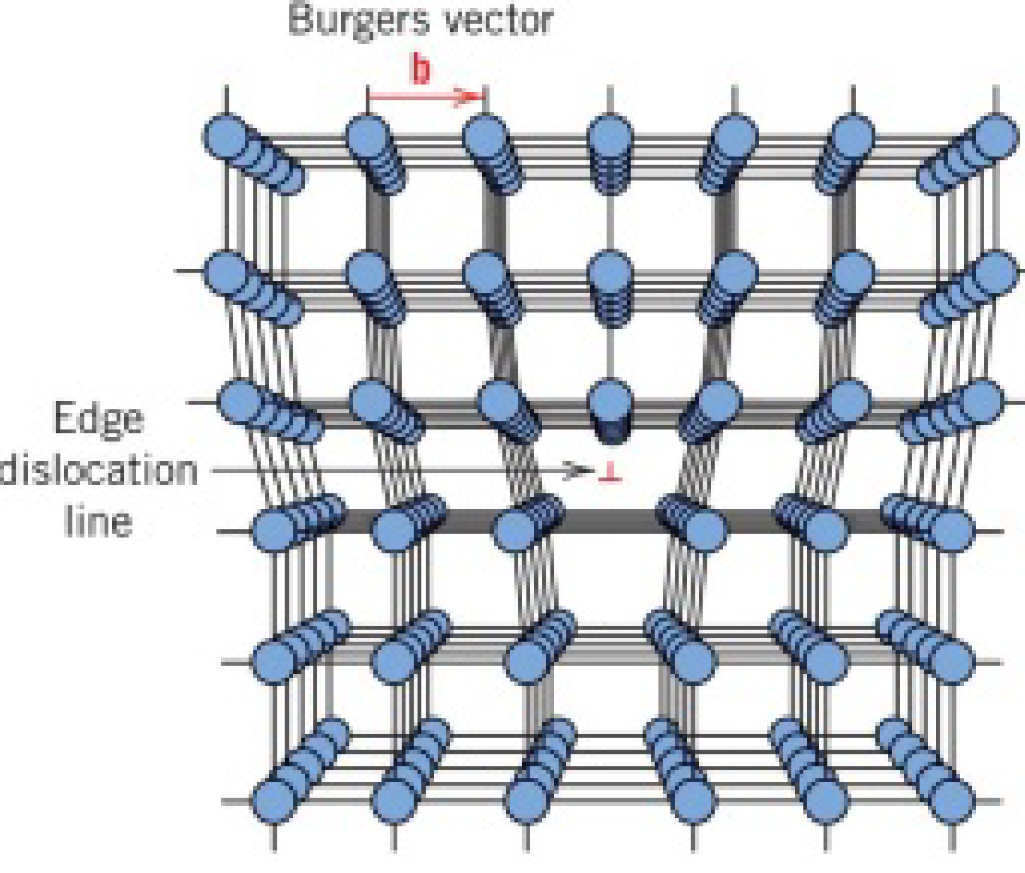
• Screw dislocation $\circlearrowright$

  

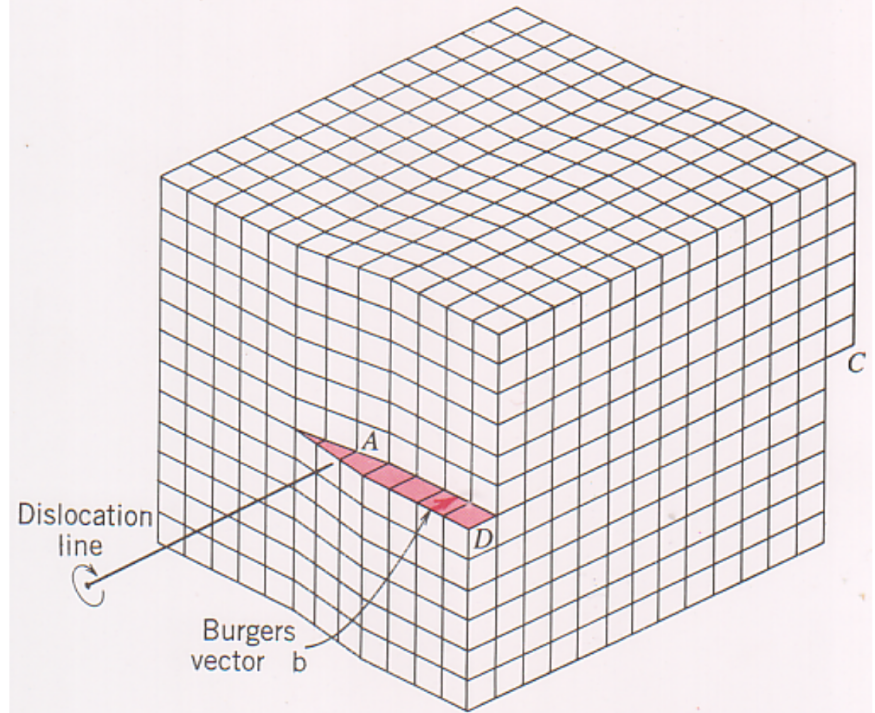
The two dislocations can mix

Interfacial defects - grain boundaries

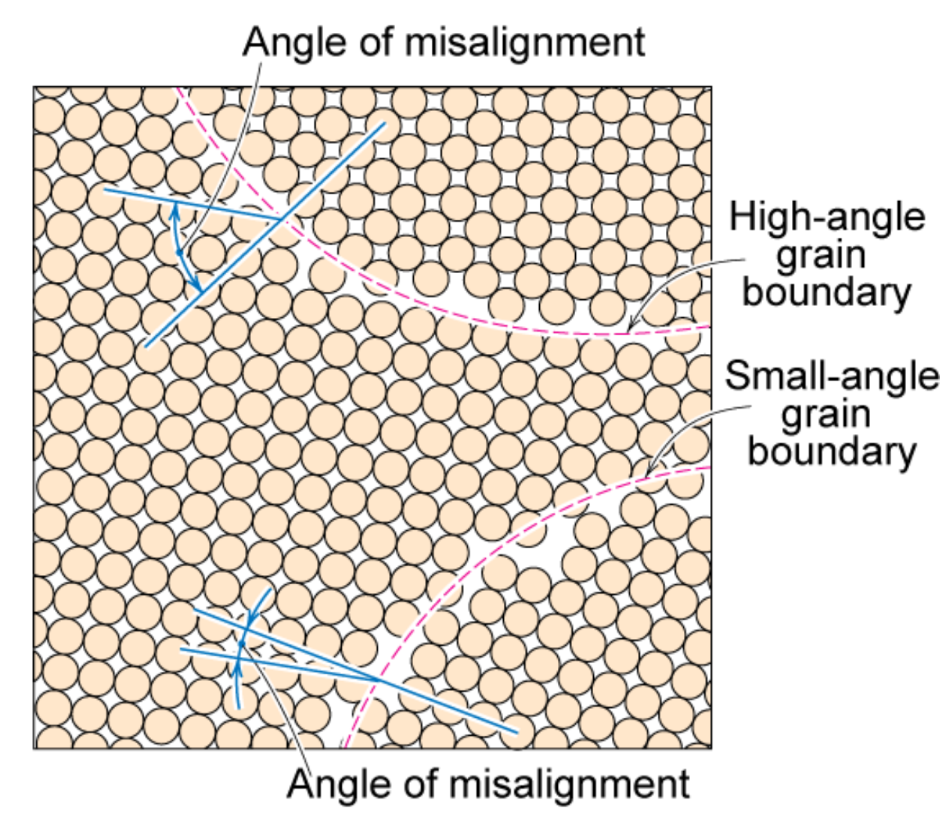Grains can be — equiaxed (similar size) & columnar (elongated grains)

• Columnar in area with less undercooling
• Equiaxed in area with rapid cooling (near wall)
• Can be large like single crystal of diamond, or small enough to require microscope Optical Microscopy — Grains
• Polishing to remove surface features (scratches)
• Etching to change reflectance depending on crystal grain orientation
  • Difference in reflectance differenciates individual grains Optical Microscopy — Grain boundaries
• The surface undergoes Acid Etching which attacks the grain boundaries
  • This shows up as dark lines under the microscope
• Polarized light can increase this contrast Electron Microscopy
• Optical resolution = 100nm
• High frequency → Higher resolution

Bulk & Volume defects

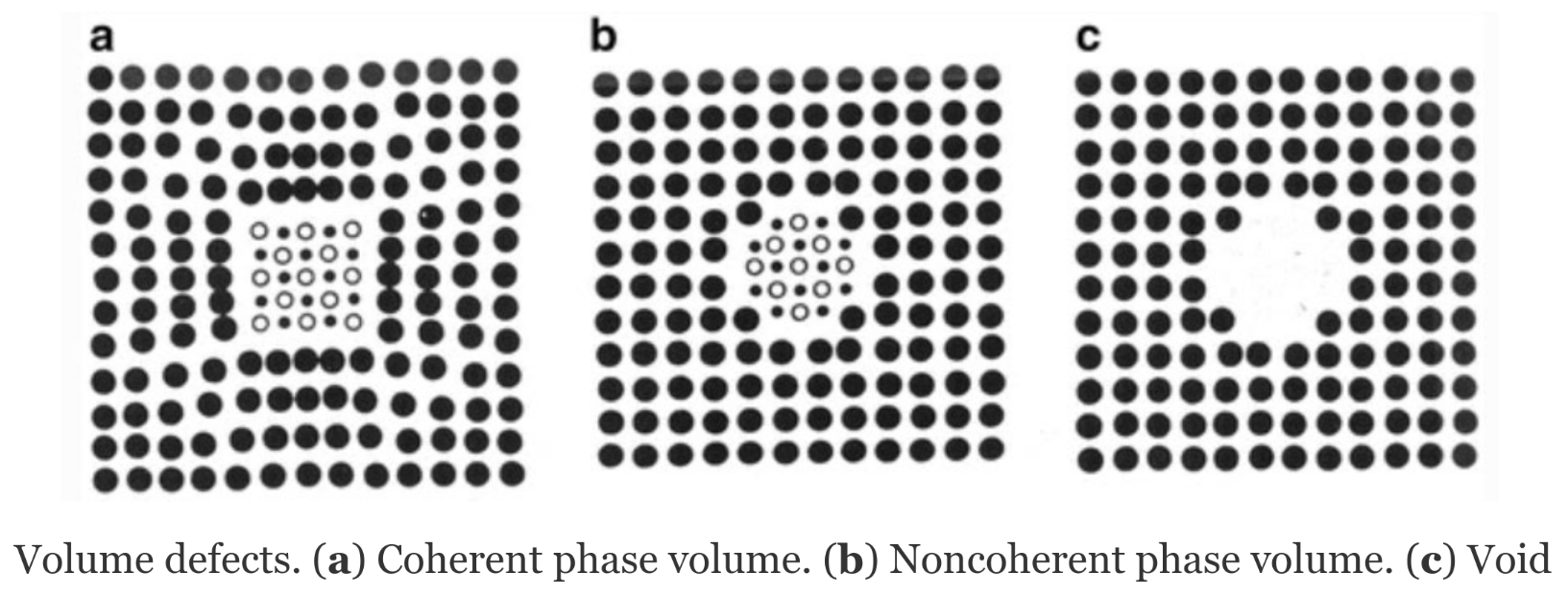
Dislocations

Plastic deformation is due to movement of dislocations — slipping in the direction of burgers vector

• Dislocations increase G proportionally to b
• Dislocations of the same sign repel while opposite signs attract and annihilate
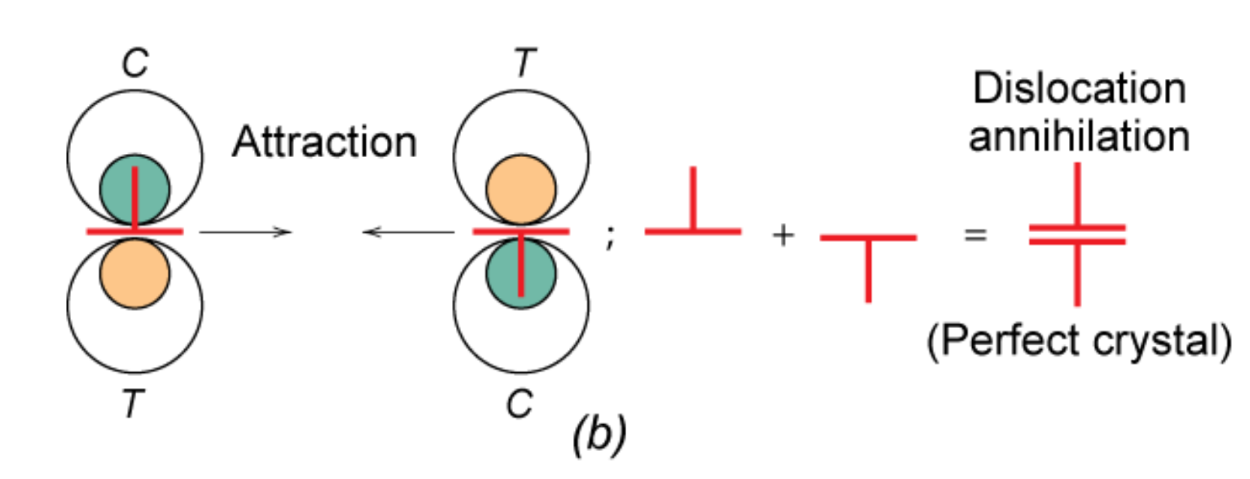
• Energy required to move dislocation is related to burgers vector b
  • Thus preferred direction is one with minimum b

Slip systems

• Slip planes — easiest slippage due to high planar density
• Slip directions — along burgers vectors

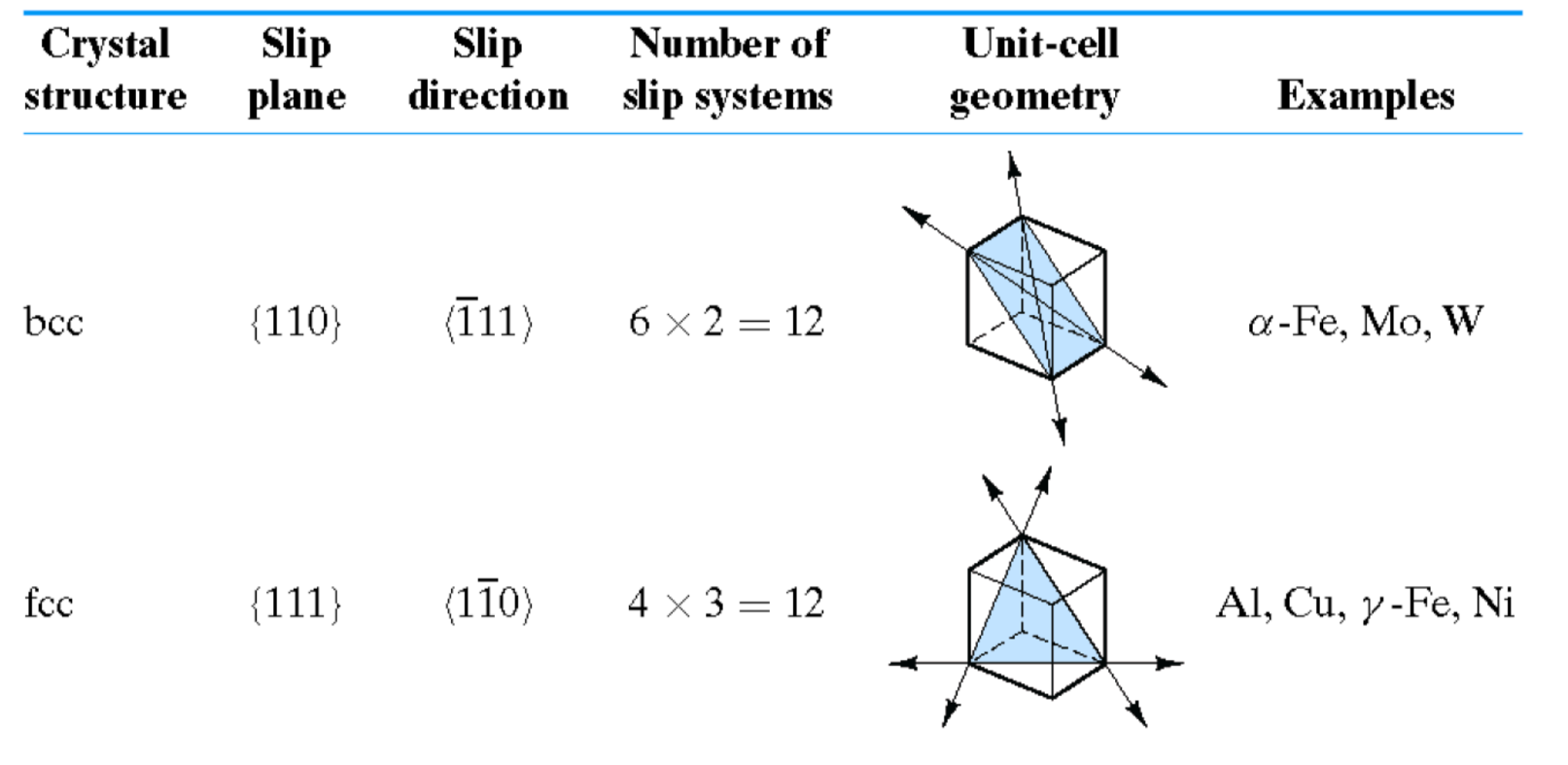
Resolved shear stress ${\tau }_r$

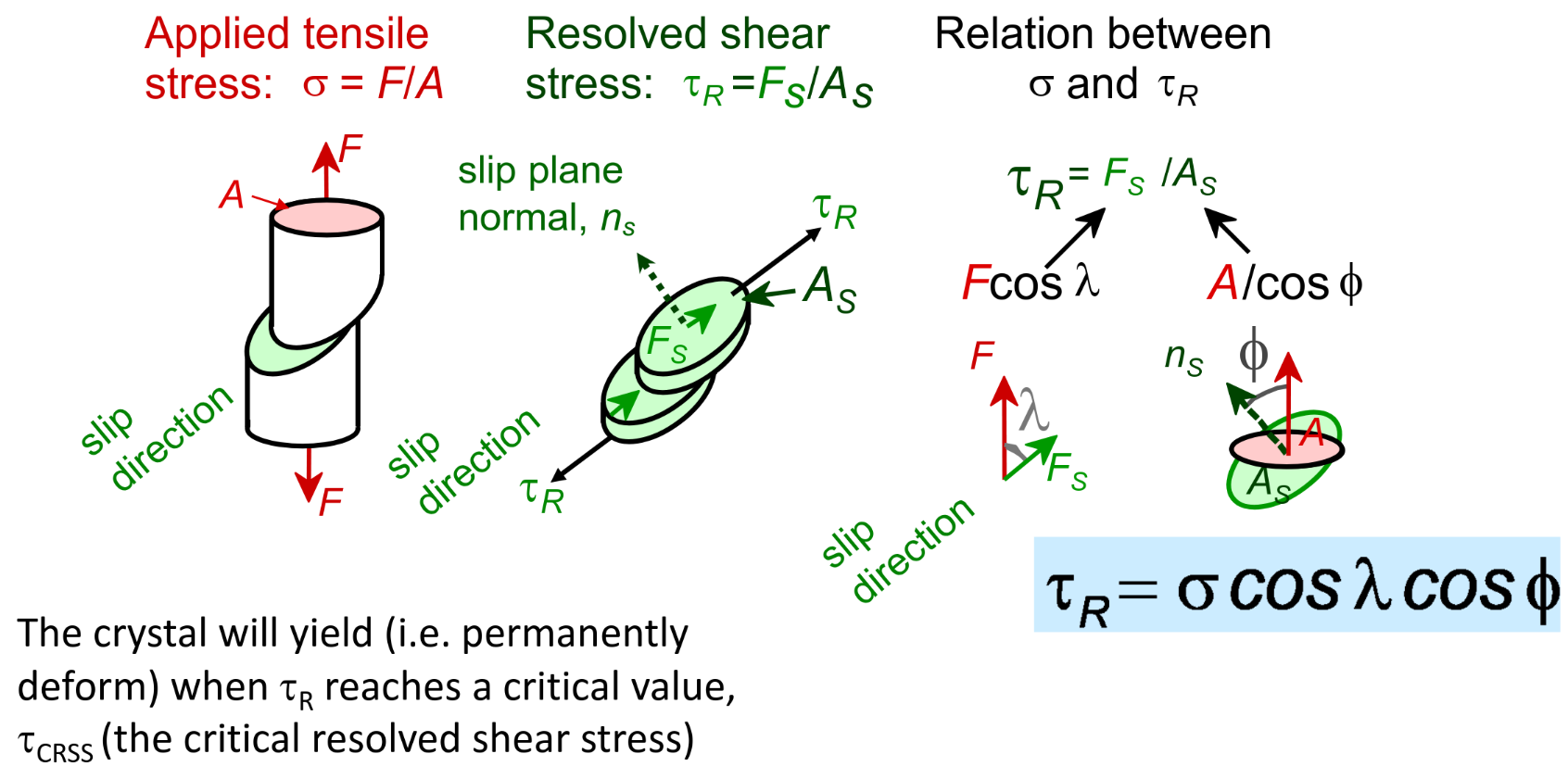
Deformation of ceramics

• Most fracture before plastic deformation

• Brittle → ionic bonds → difficult to slip due to repulsive coulombic forces between + - ions

• ionic and covalent materials are brittle and display no plastic deformation

Mechanical properties of material

Hooke’s Law: $F=-kx$ Stress($\sigma$) - strain($ϵ$): $\sigma =Eϵ$ Recap:

• Stress → force / area
• Strain → % elongation

Engineering stress

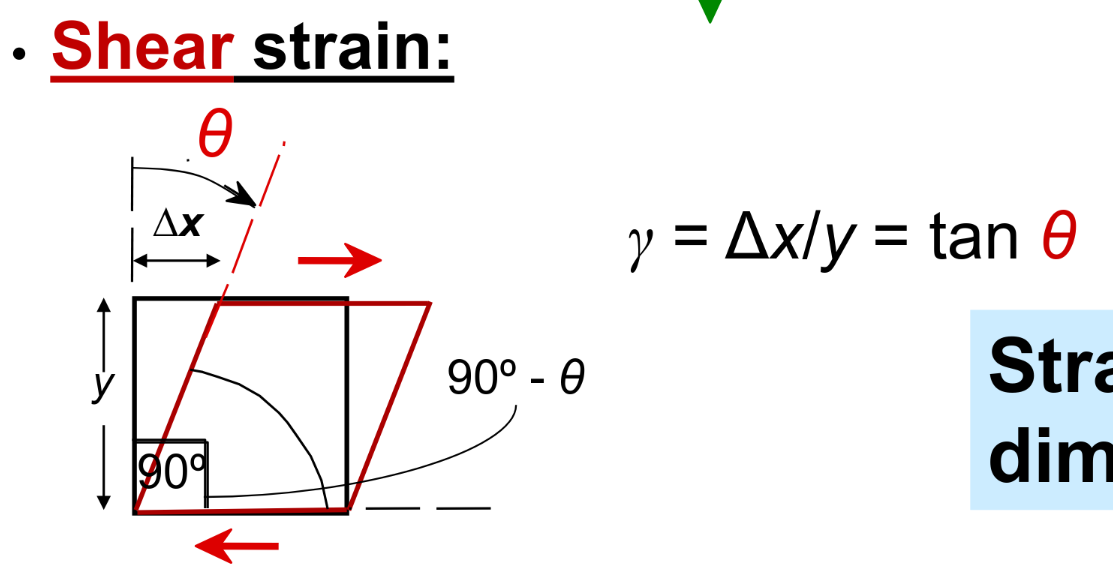
Tensile stress $\sigma$ → Stretch or compression force / area of interest Shear stress $\tau$ → shearing force / parallel area of interest

• includes torsion

Engineering strain

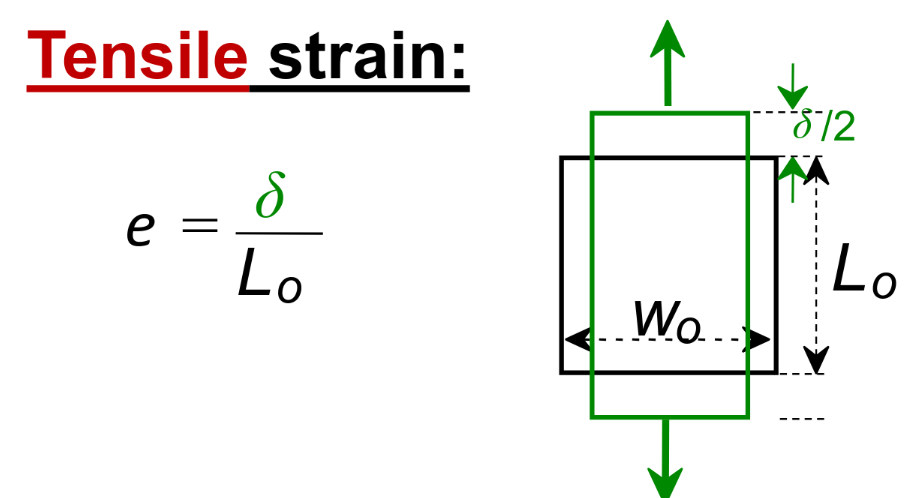
Poisson’s Ratio → a ratio describing the contraction perpendicular to extension due to tensile stress $v=-\frac{{ϵ}_x}{{ϵ}_z}$

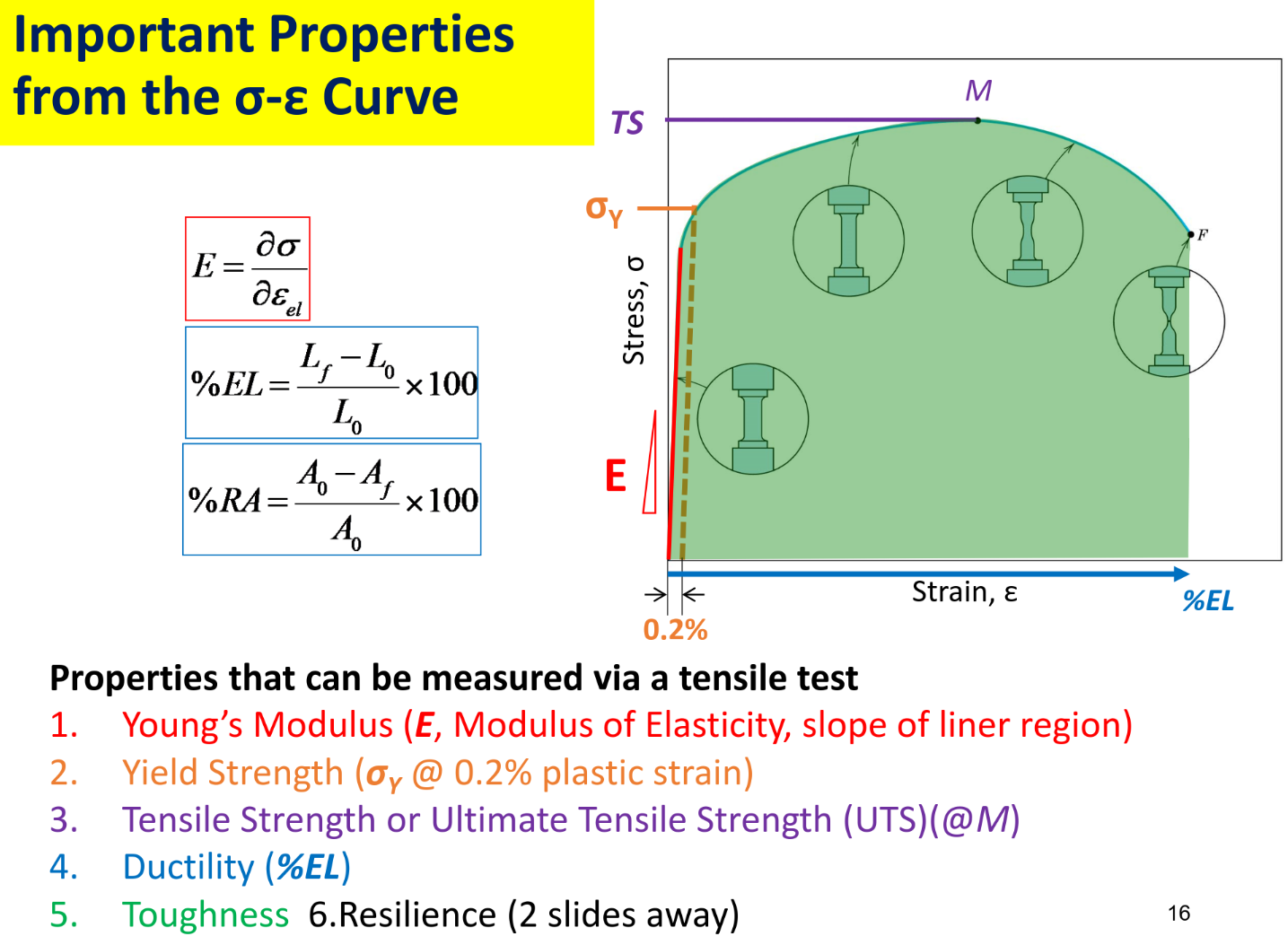
Stress-strain curve: tensile test

Resilience / Elastic strain energy $U_r$ For linear elastic: $U_r=\frac{1}{2}{\sigma }_y{ϵ}_y$

• AKA area below linear region with reference to yield strength Yield strength ${\sigma }_y$

• stress at which noticeable plastic deformation occurs

  • Happens due to slipping of planes

• Can increase with Work Hardening / Strain Hardening

  • Due to plastic deformation

    

  

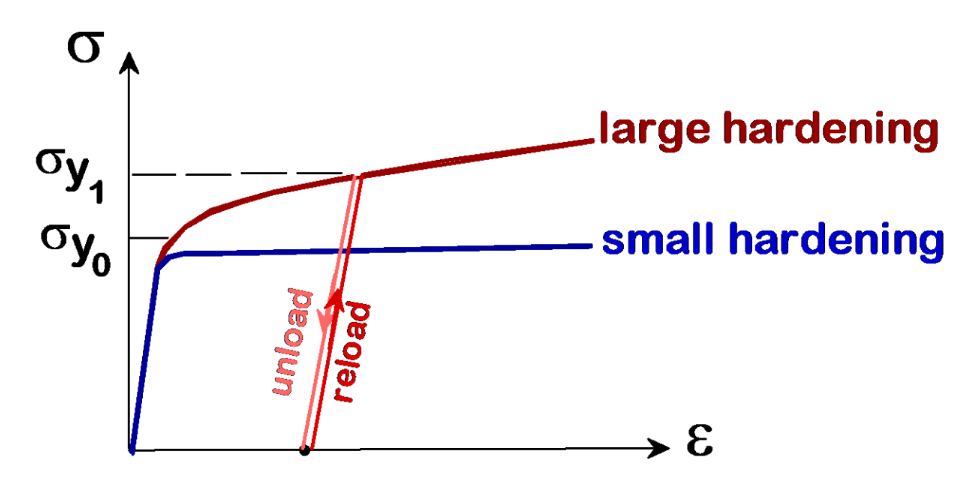
Toughness: energy required to break a unit volume of material

• Brittle(low toughness) → high yield strength but %EL — ceramics
• Tough → good yield strength and %EL — metals
• Ductile(moderate toughness) → large %EL but very low yield strength — soft polymers
• Brittle fracture — elastic energy dominant
• Ductile fracture — plastic energy dominant

True stress and strain

In the engineering graph, it curves down as the cross-sectional area rapidly decreases within neck region at the strain limits, making the material appear to weaken when it is actually strengthening

True stress vs engineering stress: ${\sigma }_T=\sigma (1+ϵ)$ True strain vs engineering strain: ${ϵ}_T=ln(1+ϵ)$

Hardness

Resistance against denting

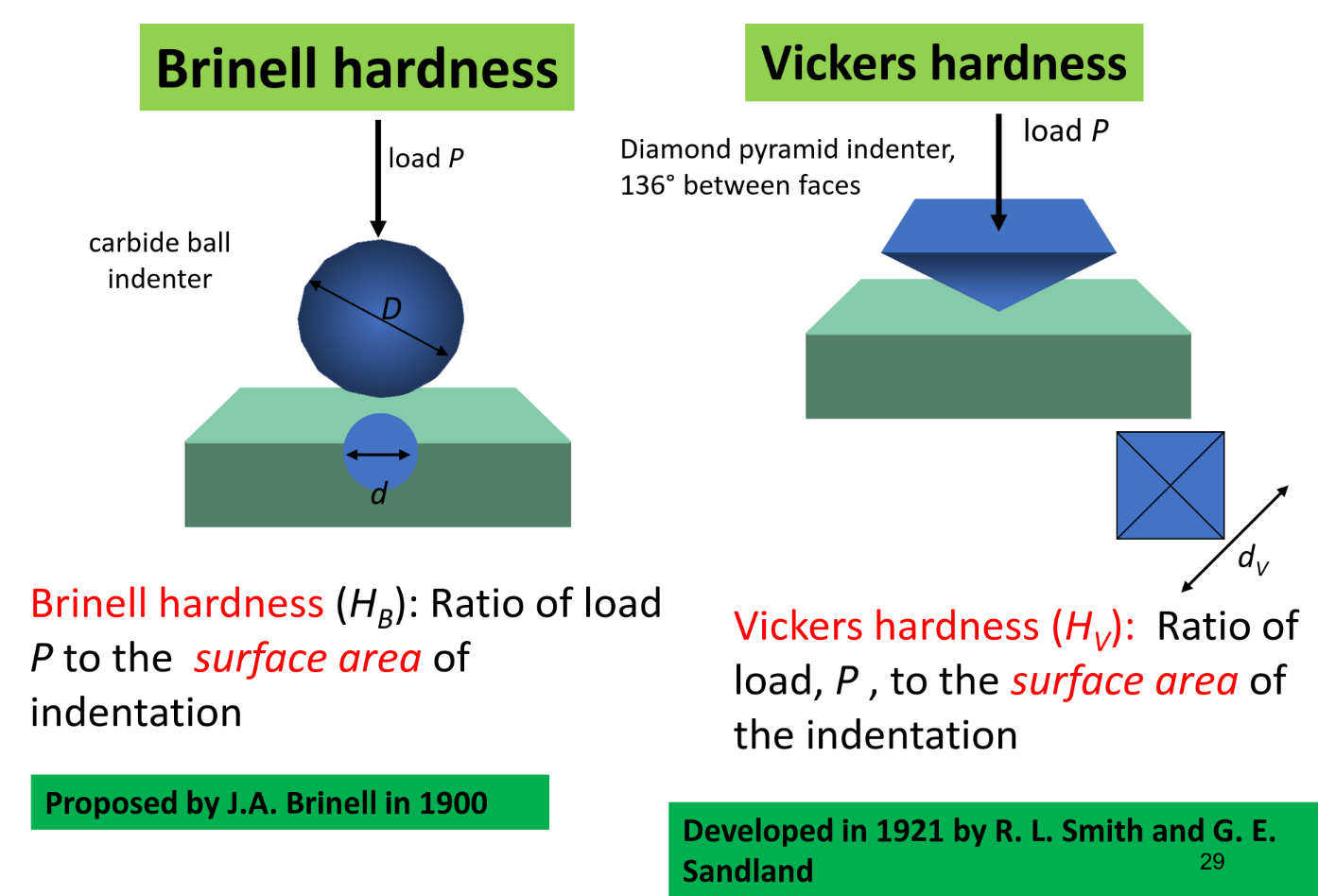Advantages of hardness test:

• Simple & inexpensive — Non-destructive — can extrapolate other data from hardness

Strengthening Mechanisms

Design principle: Increase intrinsic resistance to dislocation motion to reduce plastic deformation

Grain boundary strengthening

At < 0.5 melting temperature, grain boundaries restrict dislocation motion as it requires more energy/stress to slip past them

Smaller grain size → more barriers → higher stress to move dislocations → higher strength Hall-petch Relation ${\sigma }_y={\sigma }_0+k{D}^{-0.5}$

Solid solution strengthening

Impurities distort lattice & generate lattice strain that act as barriers to dislocation motion

• Partially cancels out compressive/tensile strength of dislocations

Strain hardening (cold work)

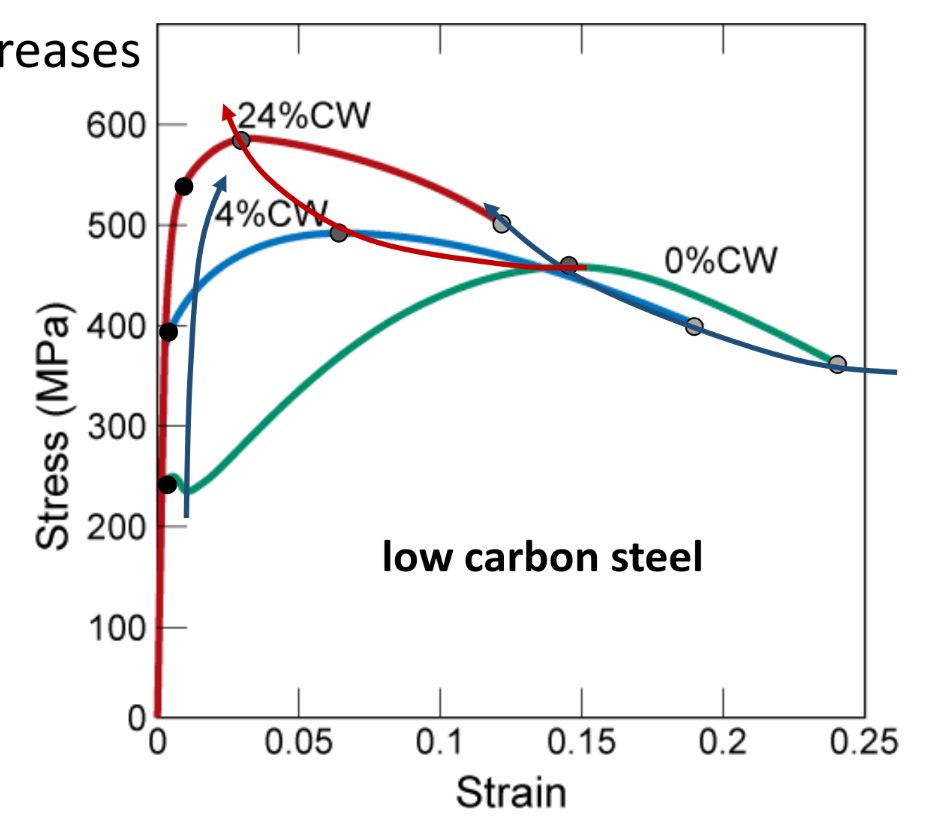Yield strength increase Tensile strength increase Ductility decrease $\%CW=\frac{A_0-A_d}{A_0}\ast 100$ $A_0=\text{initial cross section}$ $A_d=\text{resultant cross section}$

• Dislocations multiply significantly and entangle during cold work → reduced slipping
• Large deformation in cold working can make material too brittle
  • Intermittent annealing (heating and holding at high temperatures) can restore ductility for further deformations 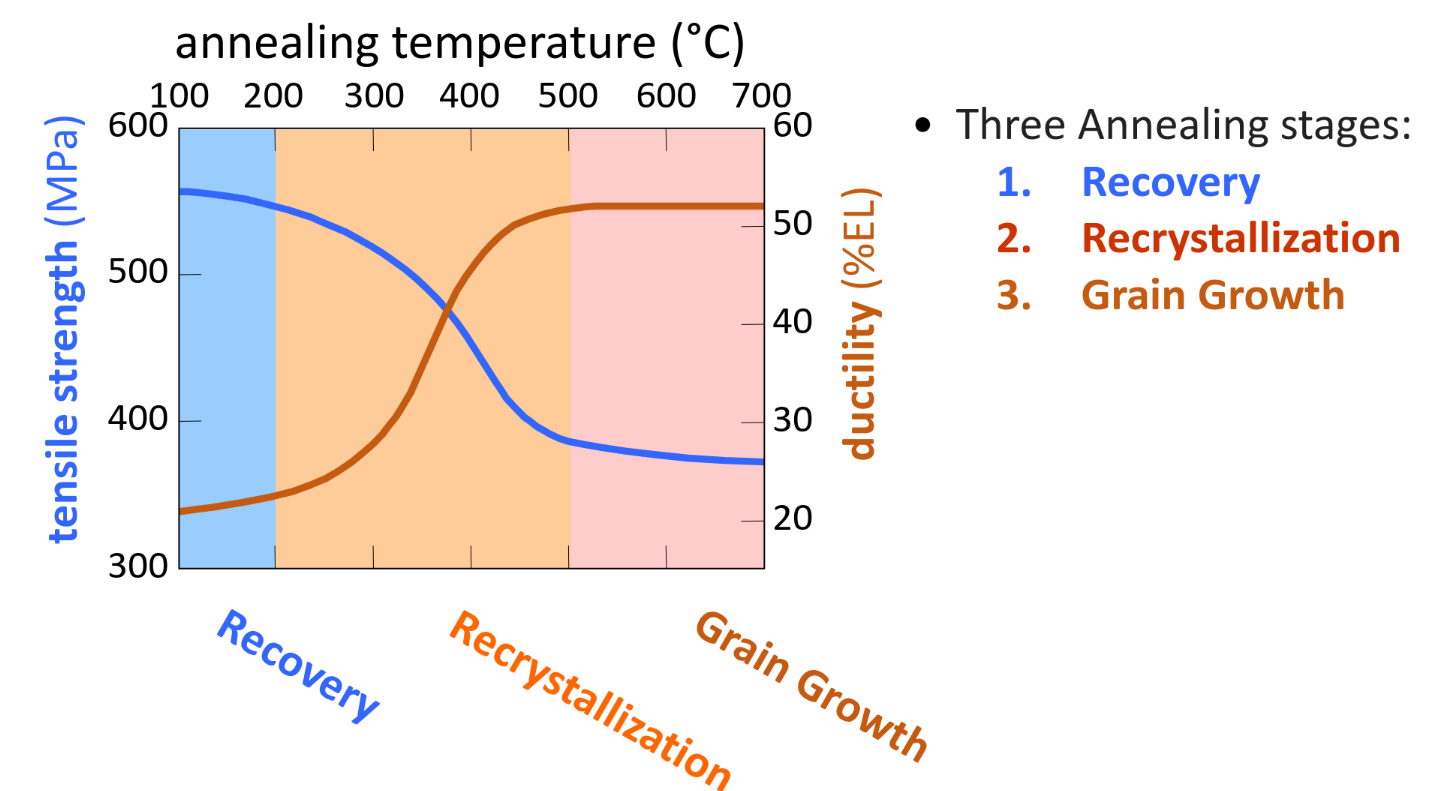Recovery — reduction of dislocation density by annihilation Results of higher temperatures:
• easier atomic diffusion → atom can move to fill area of tension
• larger vacancy concentration → allow dislocations to climb into slip plane and annihilate Recrystallisation New grains formed with:
• low dislocation density — small in size — consume and replace parent cold worked grains
• Recrystallization temperature — Temp which it completes in 1h exactly
  • $0.3T_m<T_R<0.6T_m$
  • Decreases with increasing %CW & increasing purity
  • Hot working happens above this temp Grain growth — small grain shrink and assimilate with larger grains

Phase Diagram

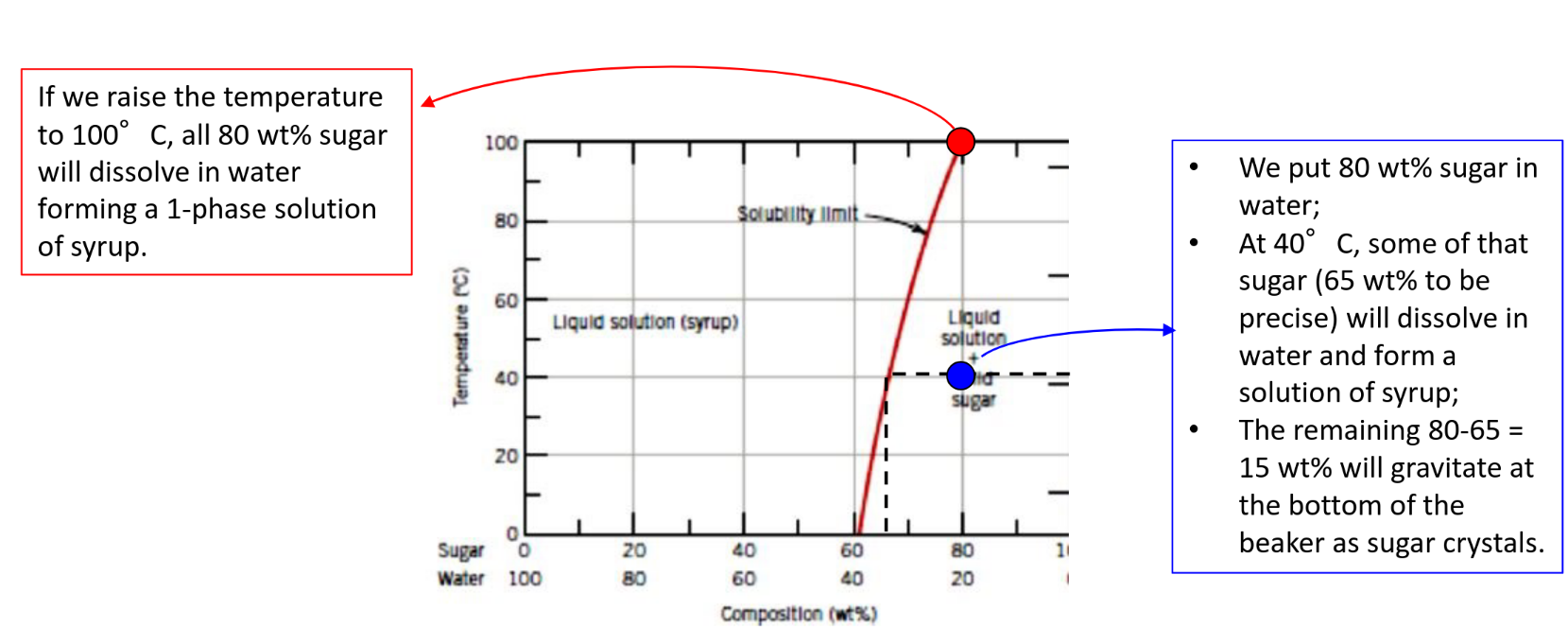
When we combine two elements, with reference to the composition and temperature, what is the resulting equilibrium states and phases?

Solubility limit — Maximum concentration for which only a single phase solution exists

Solid Solution (Alloys)

Minority = Solute — Majority = Solvent

Equilibrium phase diagrams

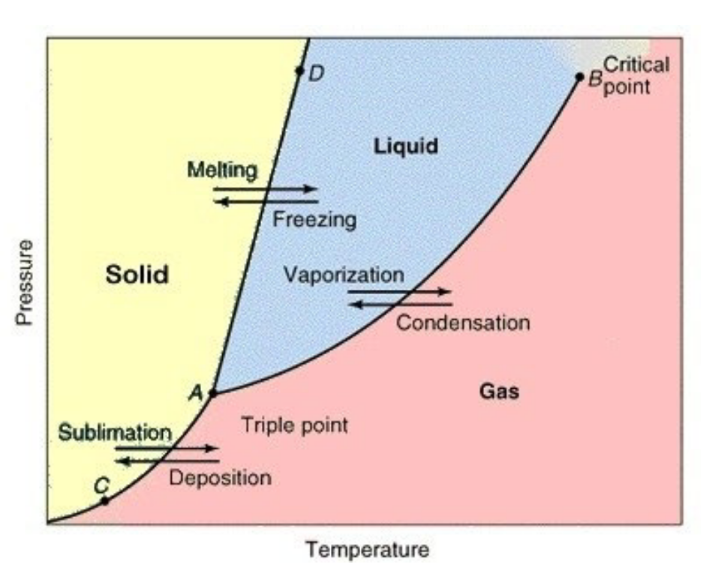
Unary Phase Diagram

Hume-Rothery rules - conditions to form complete solid solutions

1. Atomic size factor — Difference in radii < $\pm 15\%$
2. Crystal structure — same type
3. Electronegativity — similar
4. Valency — similar

Isomorphous binary phase diagram

P = 1 atm for this course 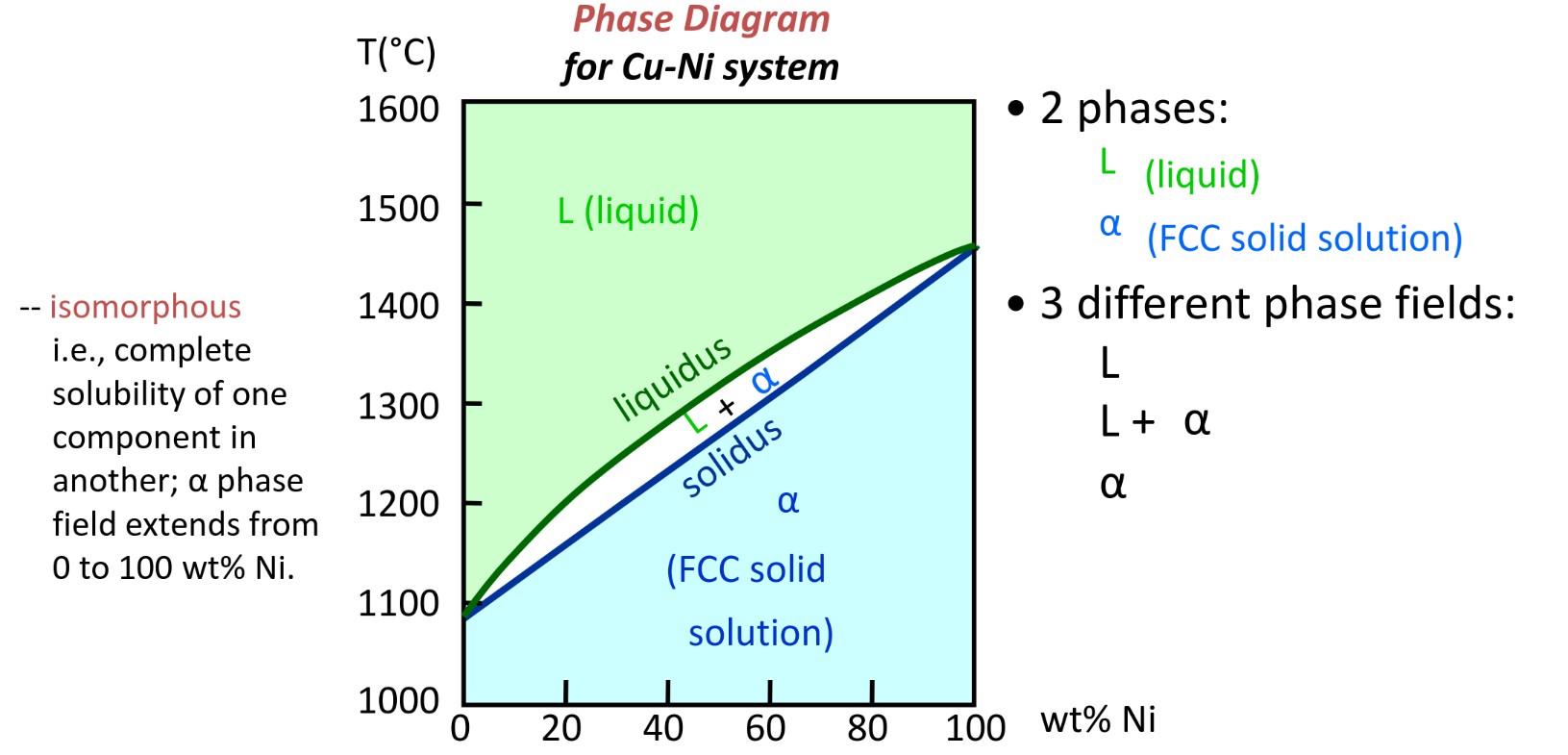Weight fraction of each phase in the mixed phase can be deduced based on graphical proximity to each state Cored vs Equilibrium phases 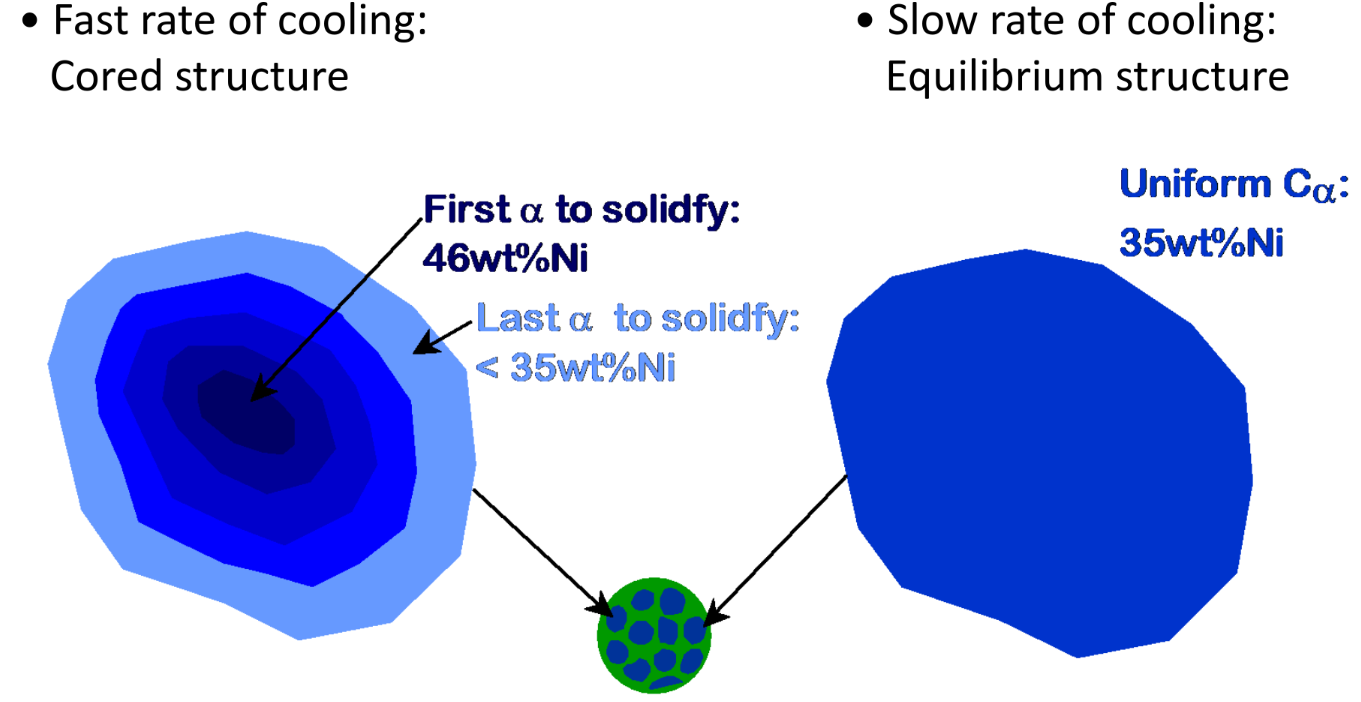Multiple phases in solid solution

Parts of the solid have different composition and crystal structure Due to: Immiscible Components — Solubility limits (Hume-Rothery rules) reached

Binary-Eutectic Systems

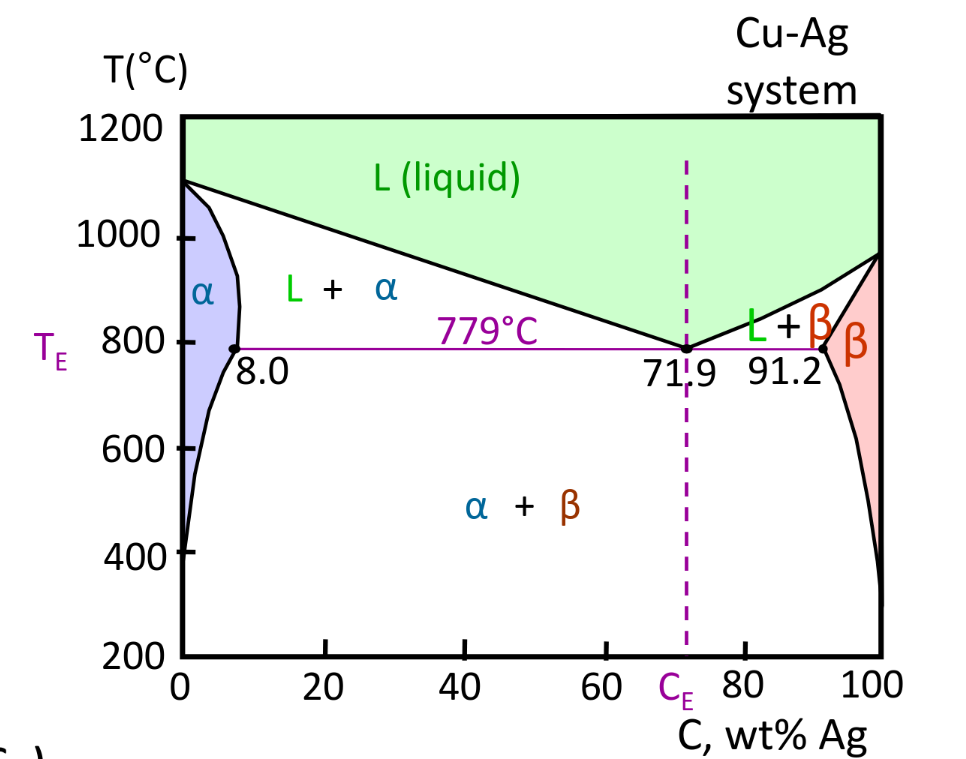
• 3 single phase regions
• Due to limited solubility
• Weight fraction is calculated the same way

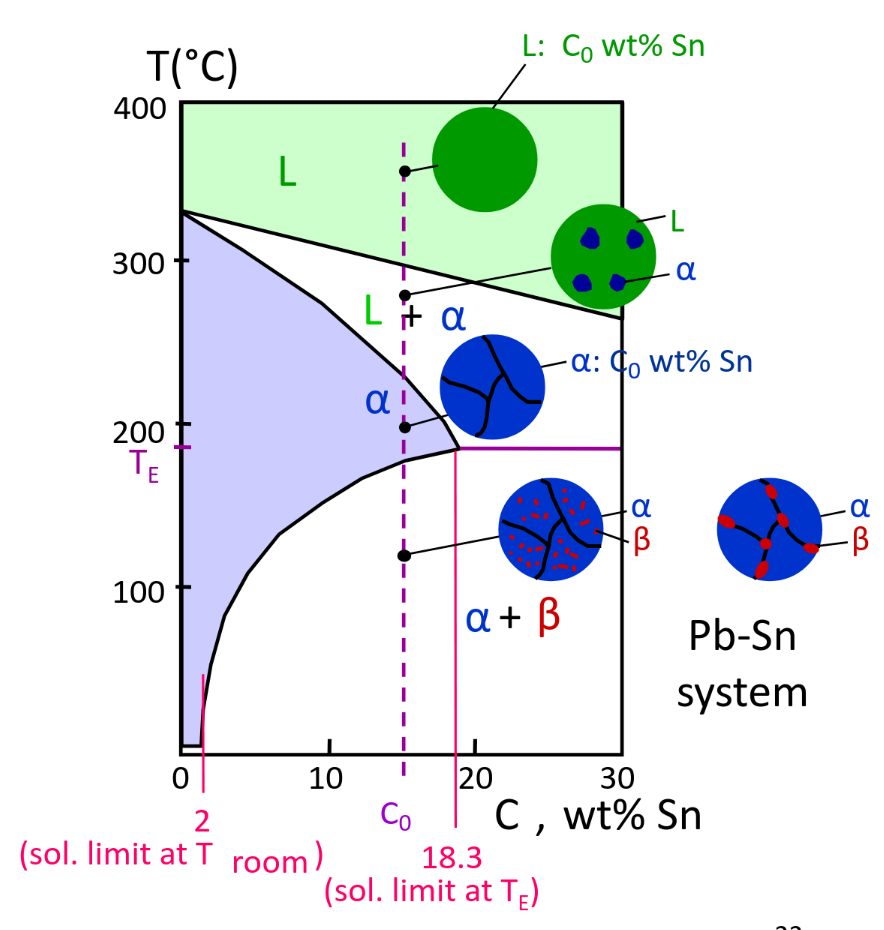
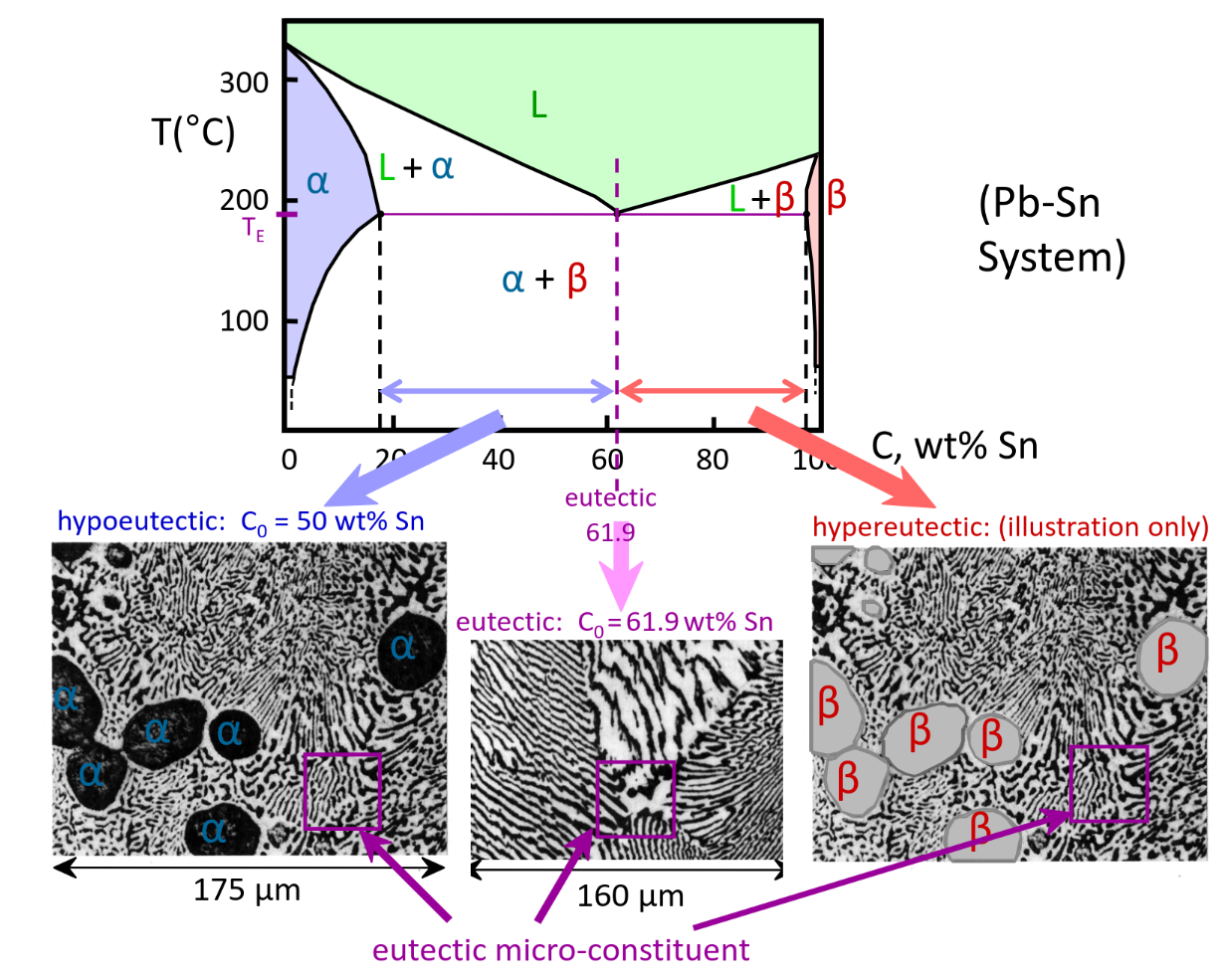
Structures in Eutectic Systems

Dual-phase Alloys

• small beta-phase precipitates

  

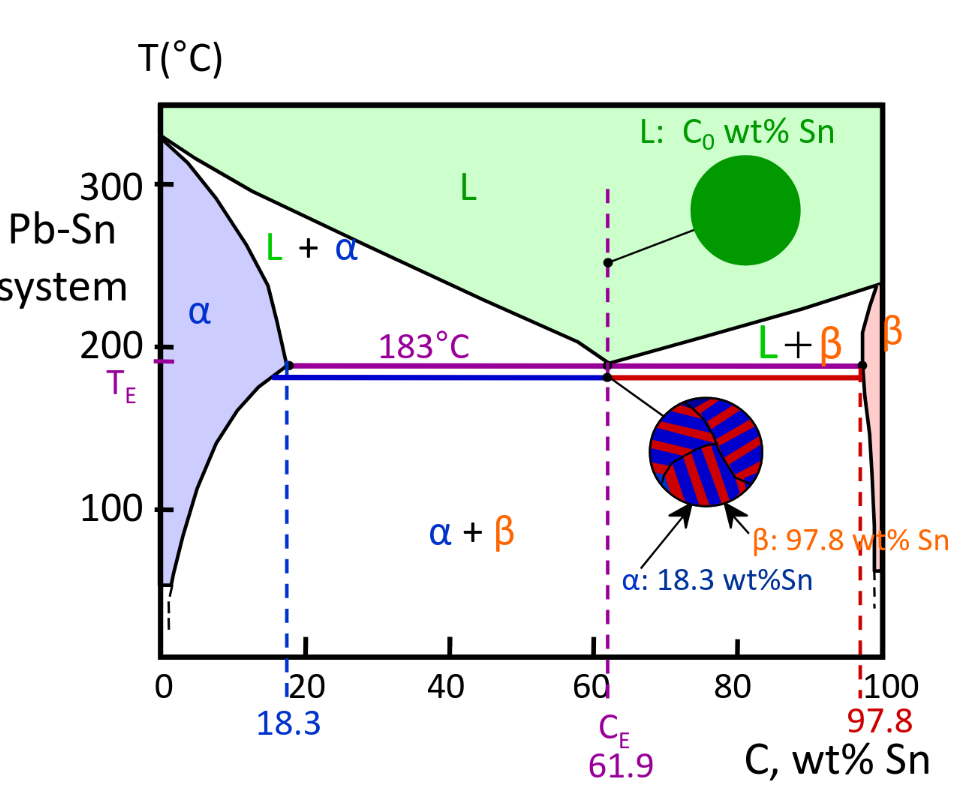
Eutectic Alloy @Ce

• Eutectic microstructure — alternating layers of alpha and beta

  

Near-eutectic Alloy — Near Ce

• particles and eutectic structure

  

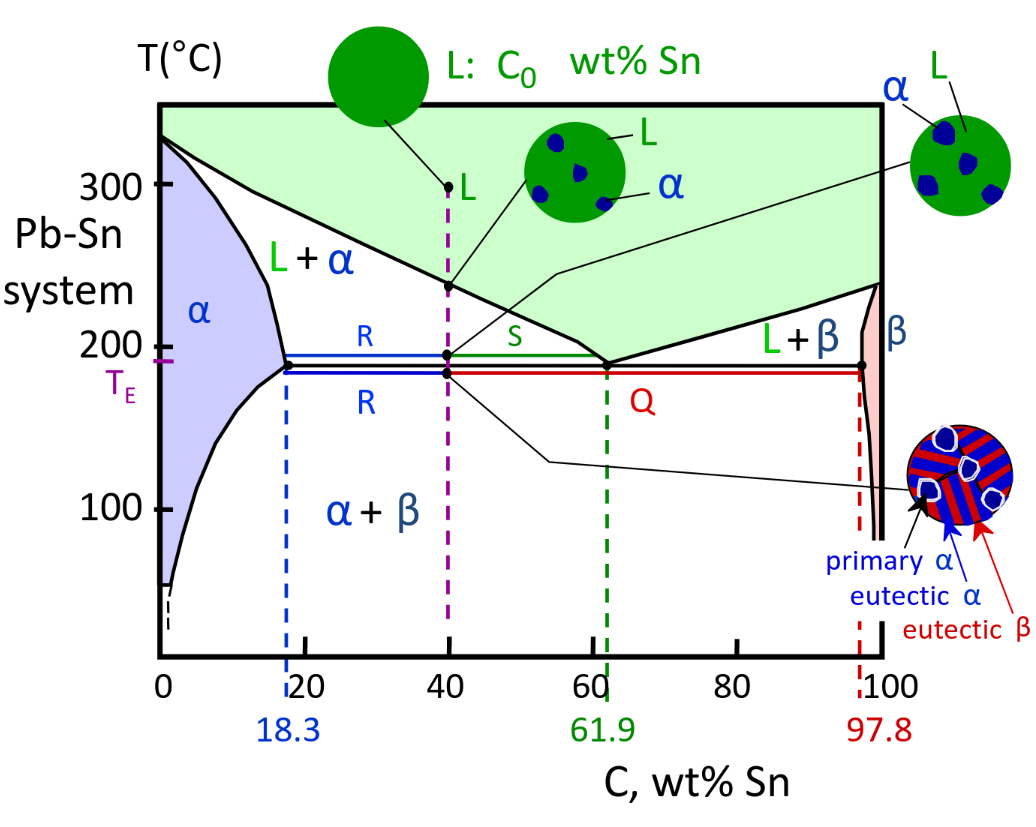
Hypoeutectic & Hypereutectic structures

Intermetallic Compounds

• Exists as a line on the diagram due to the fixed composition nature of ionic compounds (Stoichiometry)

Phase transformation

Eutectic: Liquid ↔Solid1 + Solid2 Eutectoid: Solid1 ↔ solid2 + solid3 Peritectic: Liquid + solid1 ↔ solid2

• reference

  

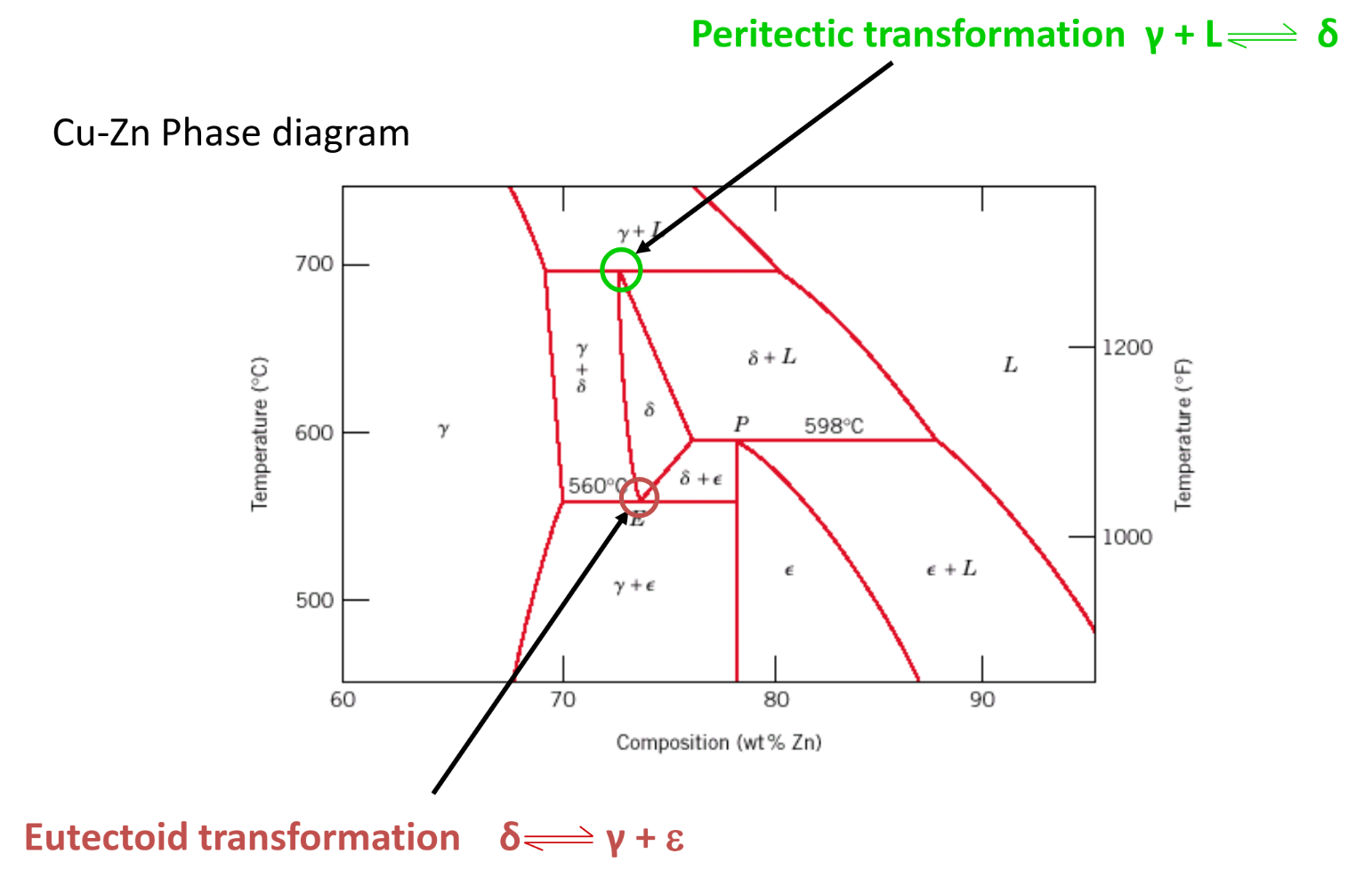
Iron-Carbon Alloys

Phase-diagram

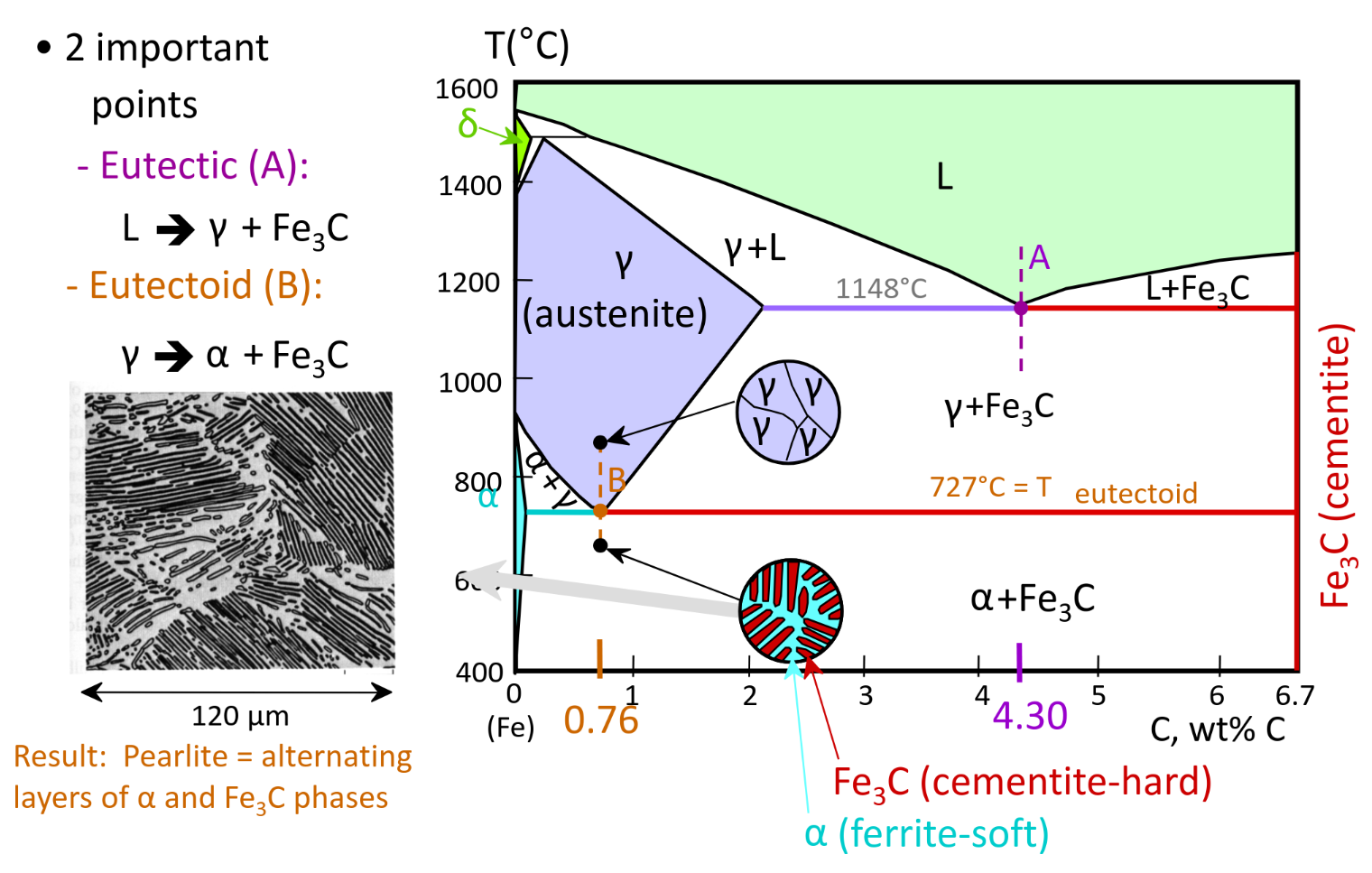Pearlite is tough and durable — rapid quenching forms Martensite, strongest and hardest in the C-Fe system (Obtained by cooling from austenite) Limitations: High density — Low electrical conductivity — Poor corrosion resistance

Steels < 1.4 wt% C

Hypoeutectoid Steel — Pearlite + Ferrite precipitate / streaks — < 0.76 wt% Hypereutectoid Steel — Pearlite + Fe3C precipitate / streaks — > 0.76 wt% 1060 steel — plain carbon steel with 0.60 wt% C

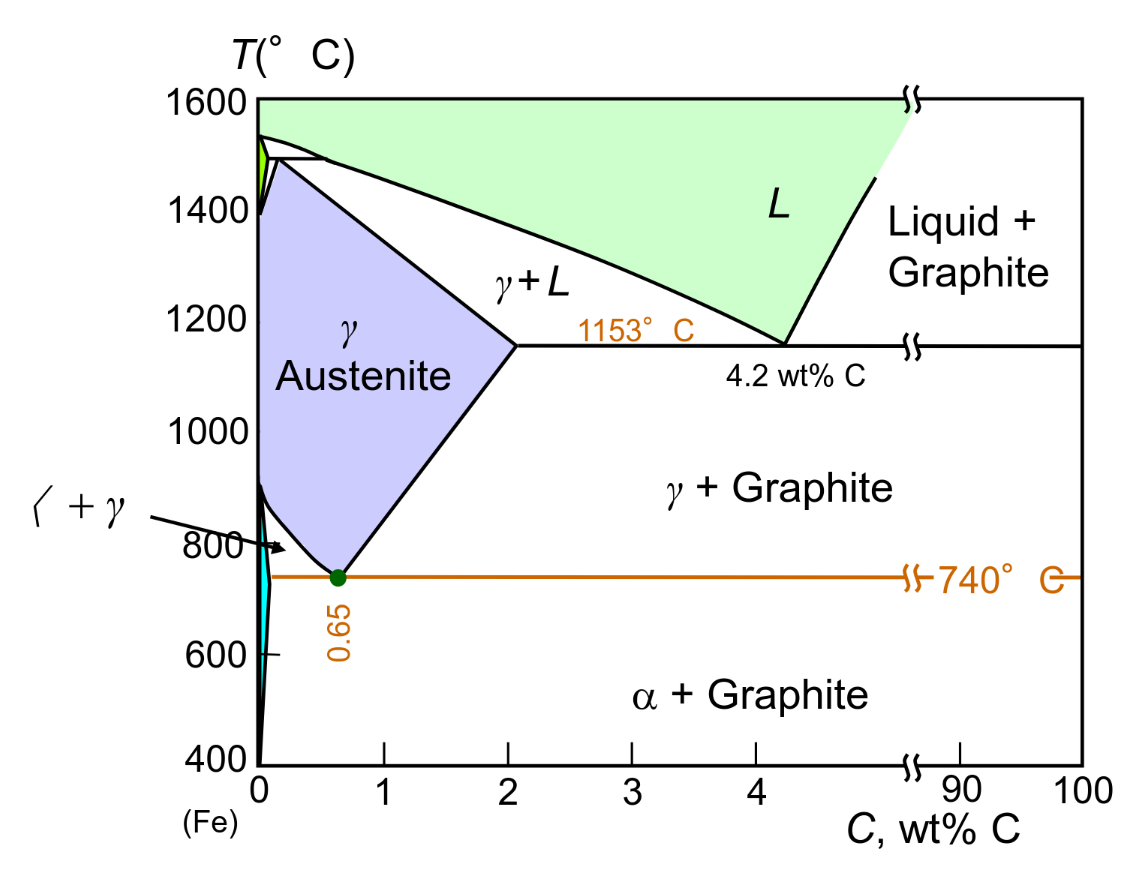
Cast Irons 3-4.5 wt% C

Brittle — Low melting — Cementite decomposes to ferrite + graphite slowly Graphite formation is promoted by Si > 1 wt% & slow cooling (True Equilibrium Diagram)

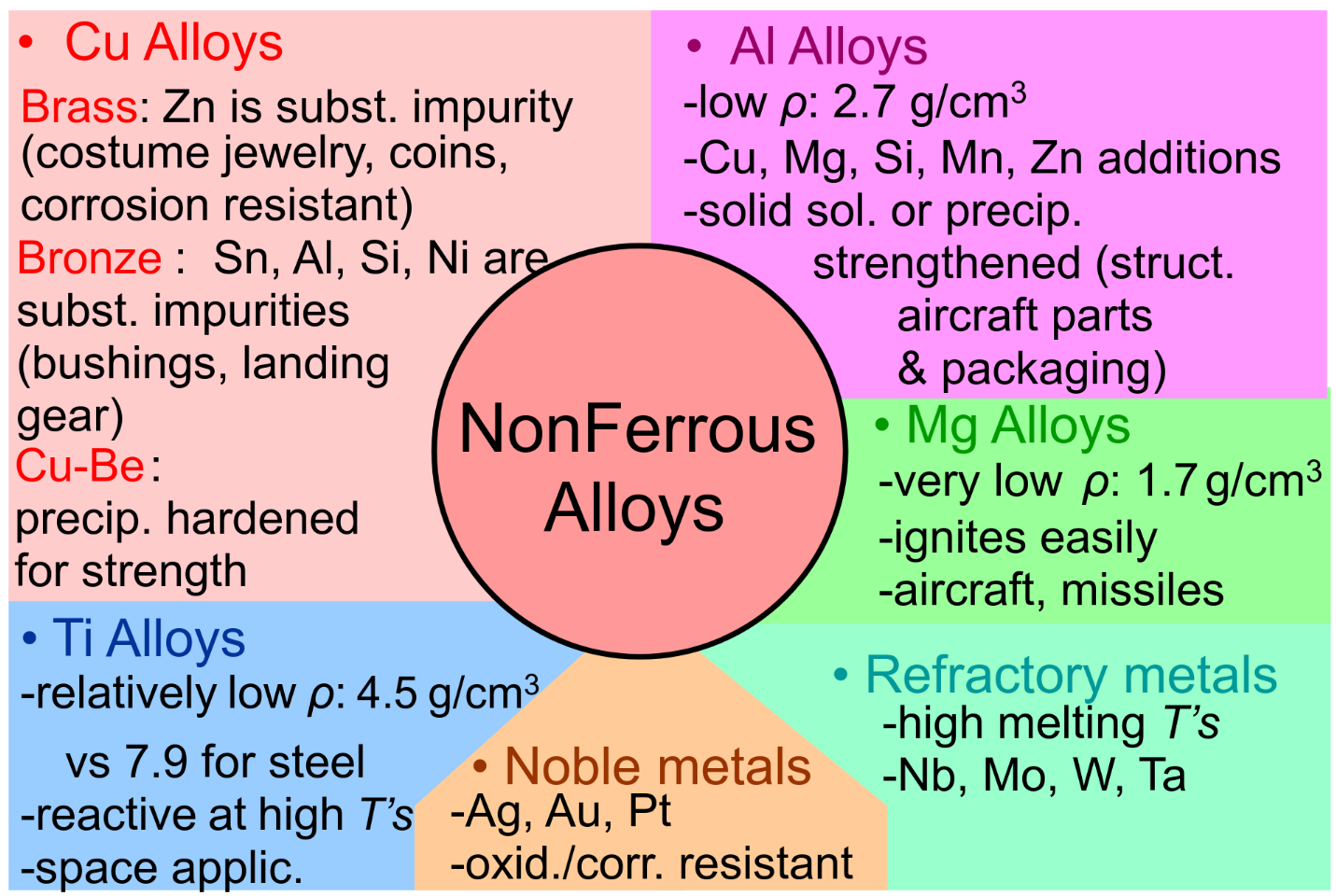
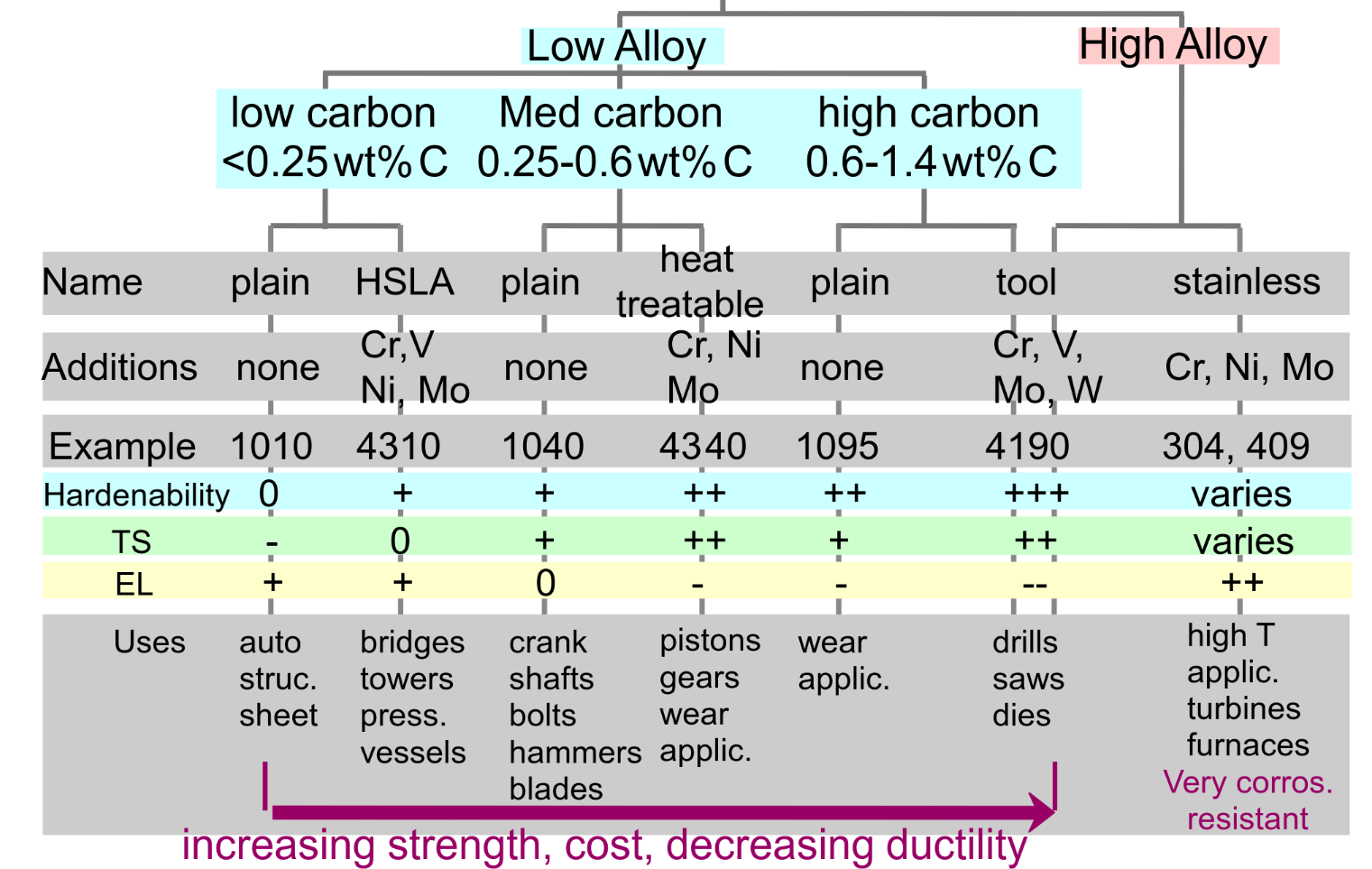
Others Non-ferrous Alloys