Artificial Intelligence

Introduction to AI

Views of AI

1. Thinking Humanly: Cognitive Modeling
   • How do humans think? Main field of neuroscience
2. Thinking Rationally: “Law of Thought”
   • Logic research - Reasoning based on logic
3. Acting Humanly: Turing test
   • To test in anonymity if a human can distinguish a machine from a human
4. Acting Rationally: Rational agents
   • Doing the right thing - Maximise goal achievement give available information
   • Main goal of this course

Complex Interactions for AI

• Stochastic, open environment - random and unpredictable
• Multiple players
• Sequential Decision, online
• Strategic (selfish) behavior
• Distributed Optimisation

Intelligent Agents

All systems / machines etc can be treated as an agent

What is an Agent?

Entity that can: Perceive through sensors - Act through effectors

Rational Agents

Rational action: action that maximises the expected value of an objective performance measure given the percept sequence to date

Rationality depends on:
• performance measure
• everything that the agent has perceived so far
• built-in knowledge about the environment
• actions that can be performed

Autonomous Agent

Adapt to the environment through experience rather than built in knowledge

Simple Reflex Agents:

• Identify rule that relates to situation
• Execute associated action Now with STATE:
• Addition: Now dependent on both situation AND stored internal state Goal-based Agents:
• Addition; Actions will continue to be performed until goals are reached Utility-based Agents:
• Addition: How happy will agent be if it attains a certain state → utility

Type of Environment

Accessible: Sensory apparatus give access to complete environmental state Deterministic: Next state is purely determined by current state and actions of agent Episodic (vs Sequential): Each episode is not affected by previous taken actions Static: Environment does not change while agent is deliberating Discrete: Limited number of distinct perceptions and actions

Design of Problem-Solving Agent

Systematically consider the expected outcome of different possible sequences of actions that lead to states of known values - Choose the best one

STEPS:

1. Goal formulation
2. Problem formulation
3. Search process
   1. No knowledge → uninformed search
   2. Knowledge → Informed search
4. Action execution (based on recommended route)

Well-Defined Formulation

Definition of problem: Information used by agent to decide what to do Specification:

• Initial state
• Action set (available actions / successor functions)
• State space (states reachable from initial)
• Goal test predicate (What indicates reaching the goal?)
• Cost function - Path cost - Sum of all actions costs along the path Solution: A path from Initial state to Goal state that satisfies the Goal-test

Measuring problem solving performance

Search cost (”offline”) - What does it cost to find the solution Execution cost (”online”) = Path cost Total cost = Search cost + Execution cost

Solving Problems by Search

Search algorithms

Frontier - candidate nodes for expansion

Explored set - set of nodes already visited

Search Strategies

A strategy is defined by picking the order of node expansion Evaluating strategies:

Completeness - Does it always find a solution is one exists?

Optimality - Does it always find the best (least-cost) solution?

Time Complexity - How long to find solution: number of nodes generated

Space Complexity - Maximum number of nodes in memory

• Branching factor

  $\frac{numberofnodes}{numberofbranches}$

Informed search

Use problem specific knowledge to guide the search

Usually more efficient Best first search - expand the most desirable unexpanded node - evaluation function Evaluation function - estimates “desirability” of each node

• Path-cost function g(n) (past experience)
  • Cost from initial state to current state (search-node) n
• Heuristic function h(n) (future prediction)
  • Estimated cost of the cheapest path from n to a goal state h(n)
  • ℎ(n) is not larger than the real cost (admissible)

Greedy Search

• Expands the node that appears to be closest to goal using h(n)

  

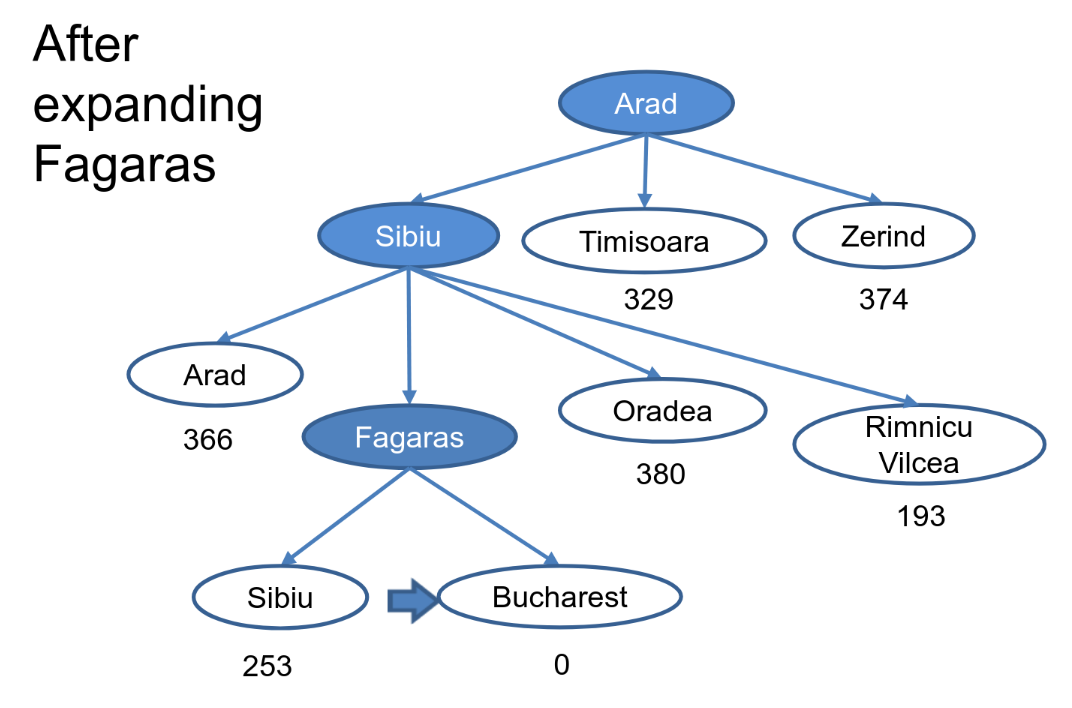
Complexity:

• Complete: no
• Time: b
• Space: b
• Optimal: No
• But still faster than uninformed searches

A * Search

Combine Greedy search with Uniform-Cost search
Evaluation function: 𝑓(𝑛) = 𝑔(𝑛) + ℎ(𝑛)

• Complexity of A*

  

Uninformed search

Use only the information available in the problem definition

Breadth-First Search

• Expand shallowest unexpanded node which can be implemented by a First-In-First-Out (FIFO) queue

  

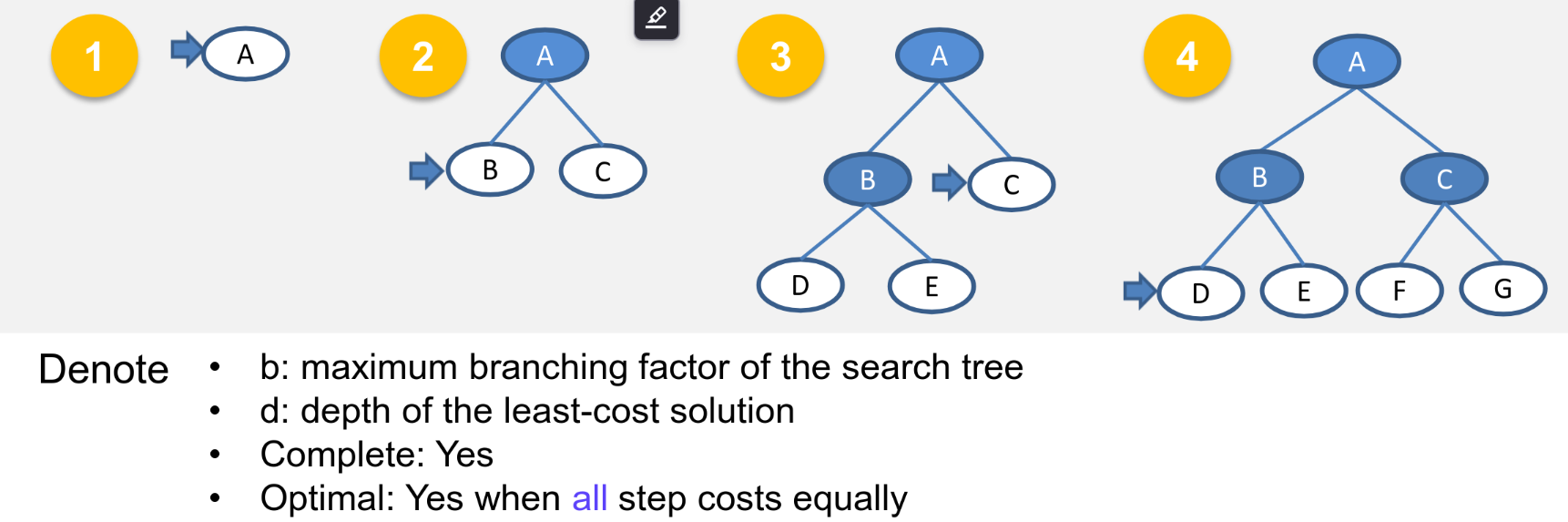
Complexity:

• $time=1+b+b^2+b^3...+b^d$

• Space = all nodes kept in memory

• Complete: Yes

• Optimal: Yes when all step costs equally

• Not suitable for deep searches

  

Denote:

• b: maximum branching factor of the search tree

• d: depth of least cost solution

Uniform-cost Search

• Consider edge costs, expand unexpanded node with the least path cost

  

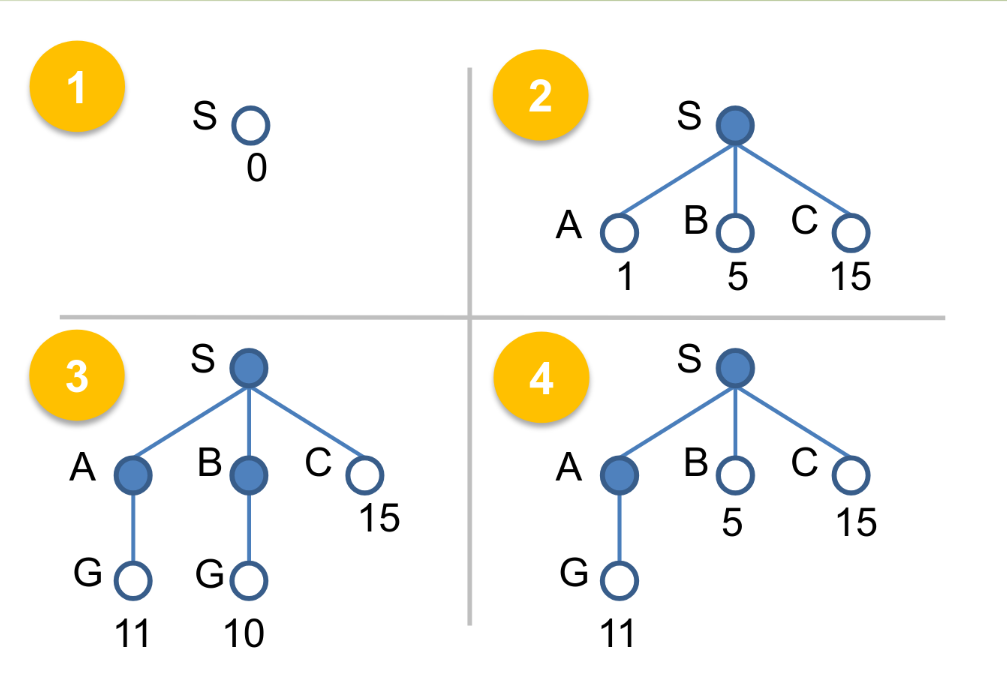
Goal test is only done when you expand to the node

Complexity:

• Complete = yes
• time = # of nodes with path cost g ⇐ cost of optimal solution
• space = # of nodes with path cost g ⇐ cost of optimal solution
• optimal = yes

Depth-first Search

• Expand deepest unexpanded node which can be implemented by a Last-In-First-Out (LIFO) stack, Backtrack only when no more expansion

  

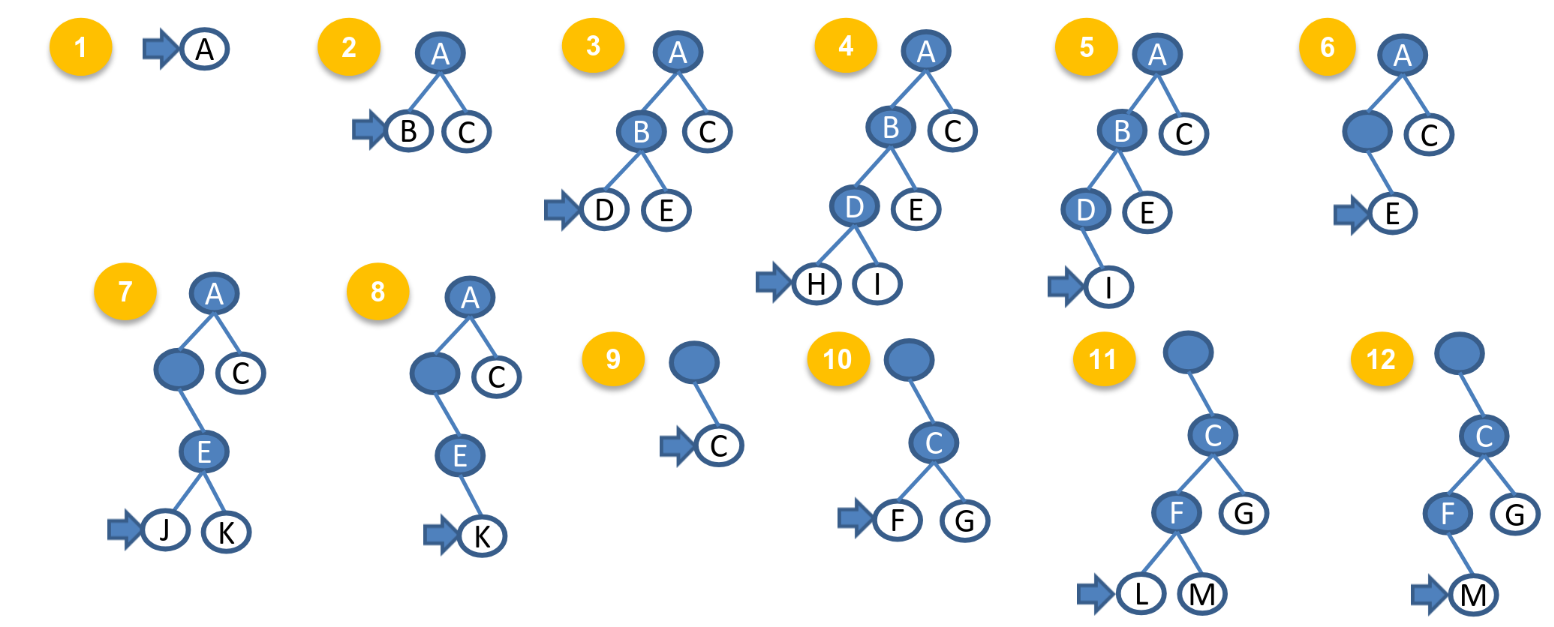
Complexity:

• Complete
  • Infinite depth = no
  • finite but loops = no
  • otherwise = yes
• Time = b
• space = b x m
• optimal = no Denote:
• m = maximum depth of the state space

Depth Limiting: To avoid infinite searching, Depth-first search with a cutoff on the max depth I of a path Complexity:

• Complete = yes if I ≥ d

• Time = b

• Space = b x I

• Optimal = no Iterative deepening search:

• Iteratively estimate the max depth / of DLS one-by-one

  

  

  

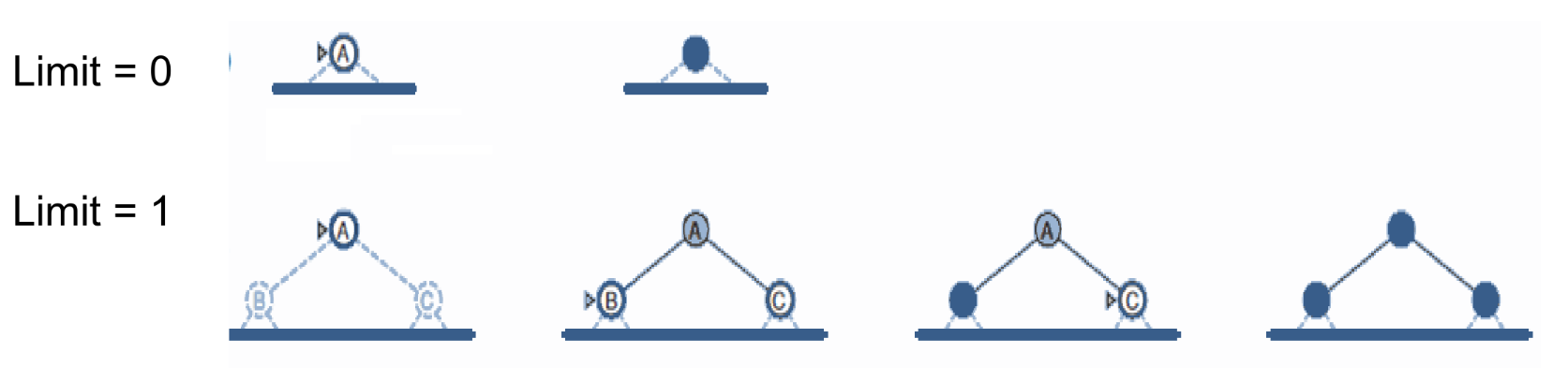
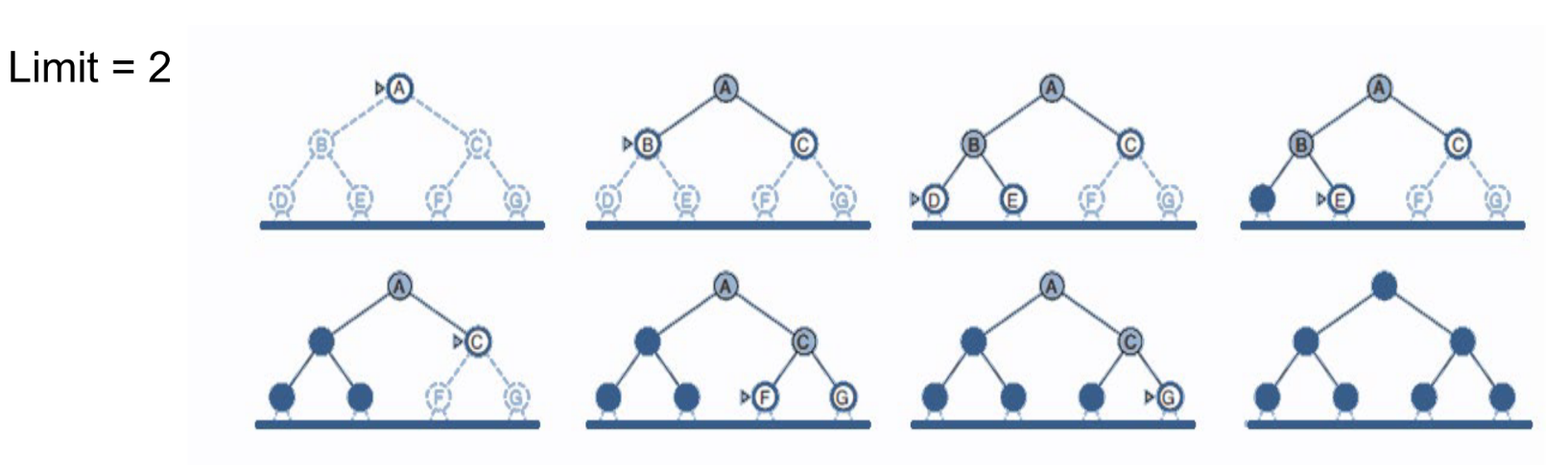
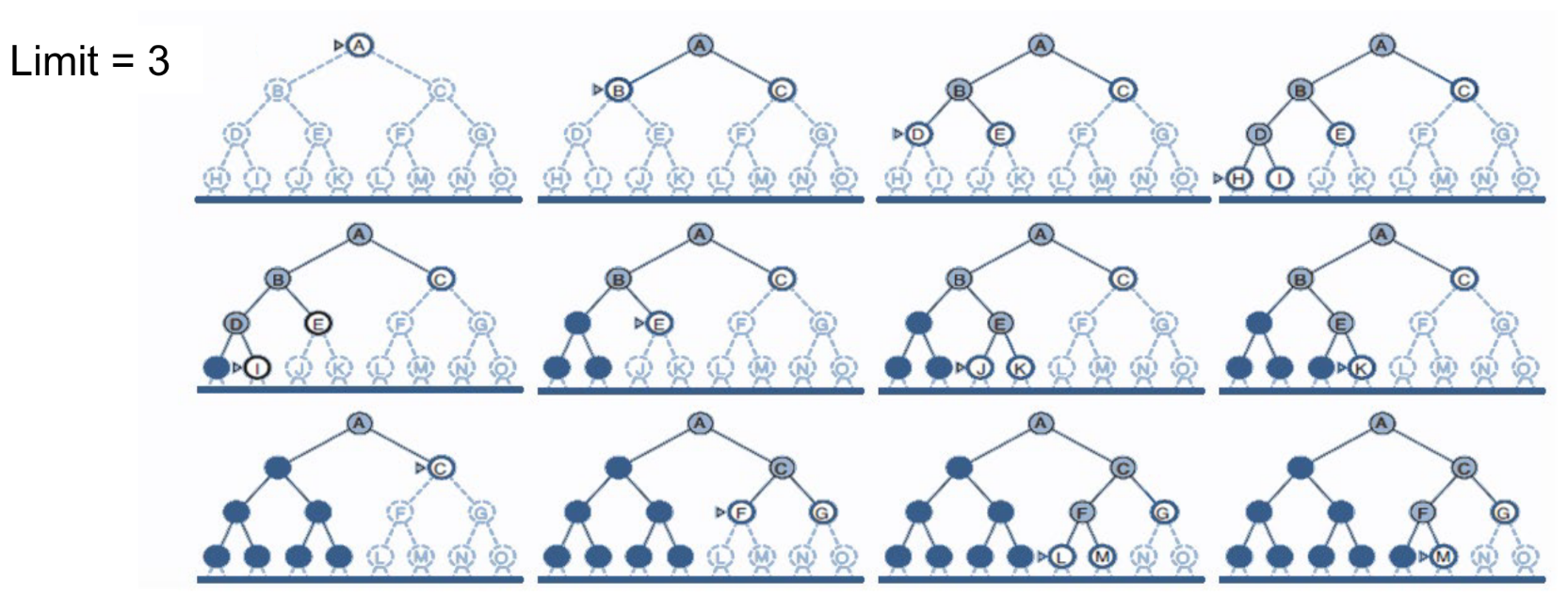
Summary

Constraint Satisfaction and Game playing

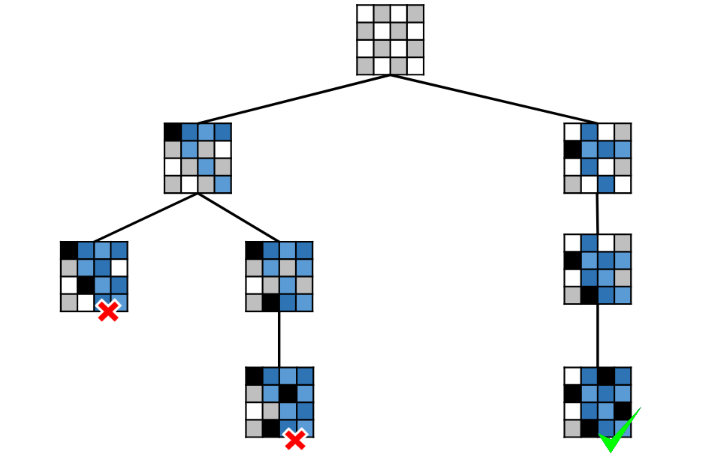
Constraint Satisfaction Problem (CSP)

Goal: discover some state that satisfies a given set of constraints

State: defined by variables $V_i$ with values from domain $D_i$ Goal test: a set of constraints specifying allowable combinations of values for subsets of
variables

• Some Definition
  • A state of the problem is defined by an assignment of values to some or all of the variables.
  • An assignment that does not violate any constraints is called a consistent or legal assignment
  • A solution to a CSP is an assignment with every variable given a value (complete) and the assignment satisfies all the constraints.

Backtracking search - Uninformed

Do not waste time searching when constraints have already been violated

1. Before generating successors, check for constraint violations
2. If yes, backtrack to something else

Heuristics for CSP

Implication of current variable assignments for other unassigned variables - Constraint Propagation

• E.g.

  

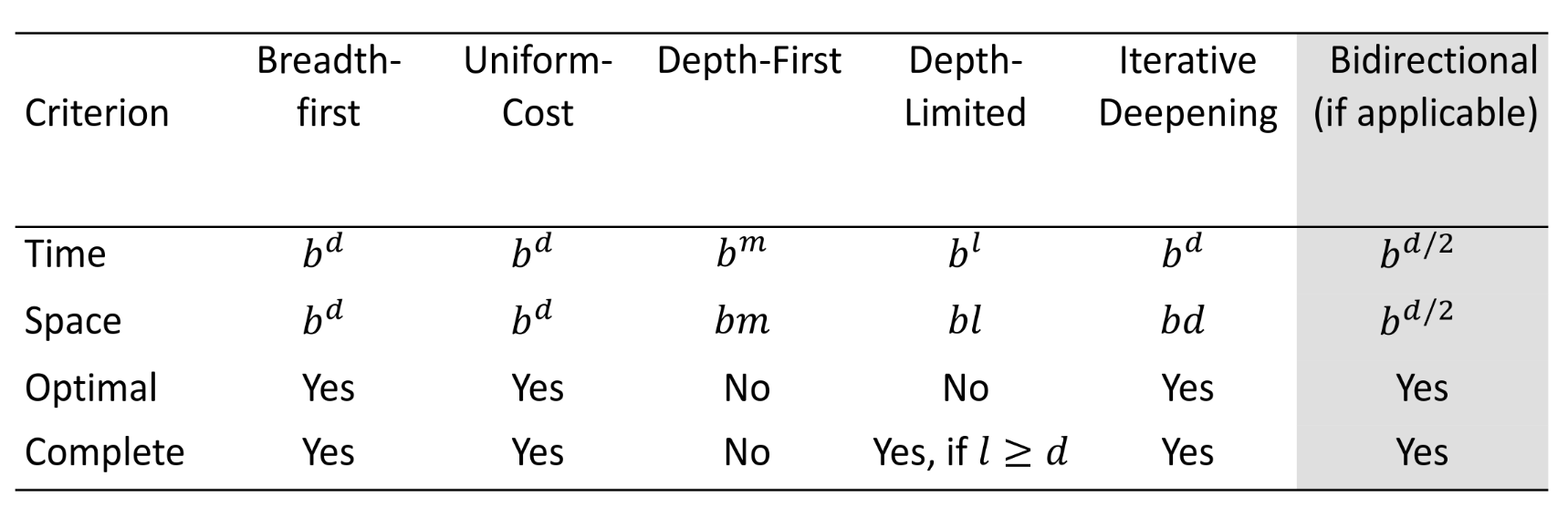
Which variable to assign next - Most Constrained Variable

• To reduce the branching factor on future choices by selecting the variable that in involved in the largest number of constraints on unassigned variables

  

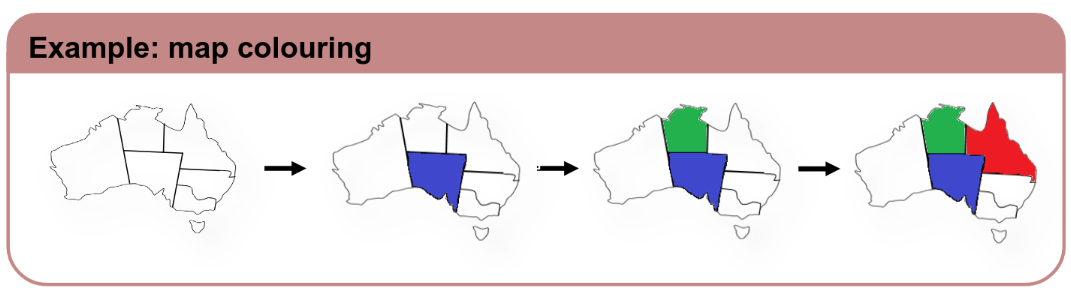
What order of values to try for each variable - Least Constraining Value

• Choose the value that leaves maximum flexibility for subsequent variable assignments

  

Min-Conflict Heuristic - CSP Method

• Given an initial assignment, selects a variable in the scope of a violated constraint and assigns it to the value that minimises the number of violated constraints

Game Playing

Why games?

Abstraction - Ideal representation of a real world problem Uncertainty - existence of hostile agents (players)

• Contingency problem - plans have to alter based on hostile agent actions Complexity - Games are abstract but not simple + Time limited
• Key terminology
  • Initial state: initial board configuration and indication of who makes the first move
  • Operators: legal moves
  • Terminal test: determines when the game is over
    • states where the game has ended: terminal states
  • Utility function (payoff function): returns a numeric score to quantify the outcome of a game

Minimax Search Strategies

Maximise one’s own utility and minimise the opponent’s

• Assuming opponent does the same 3-step Process

1. Generate the entire game tree down to terminal states
2. Calculate utility for all states / process
3. Select best move (Highest utility value) Perfect decisions? No time limit - Complete Search Tree Move chosen achieves best payoff assuming best play Imperfect decisions?

Time/space requirement → complete game tree is intractable → impractical to make perfect decisions Modification to minimax algorithm

1. replace utility function with evaluation function (estimated desirability)
2. partial tree search
   1. depth limit
   2. replace terminal test with cut-off test